功能

基本操作

以滑鼠控制滑動尺、上下鍵，可快速變更膜厚、折射率。
就能同時顯示多種曲線圖，從各種視點進行薄膜設計。
多張標籤工作表，最多可同時設計20個膜資料。

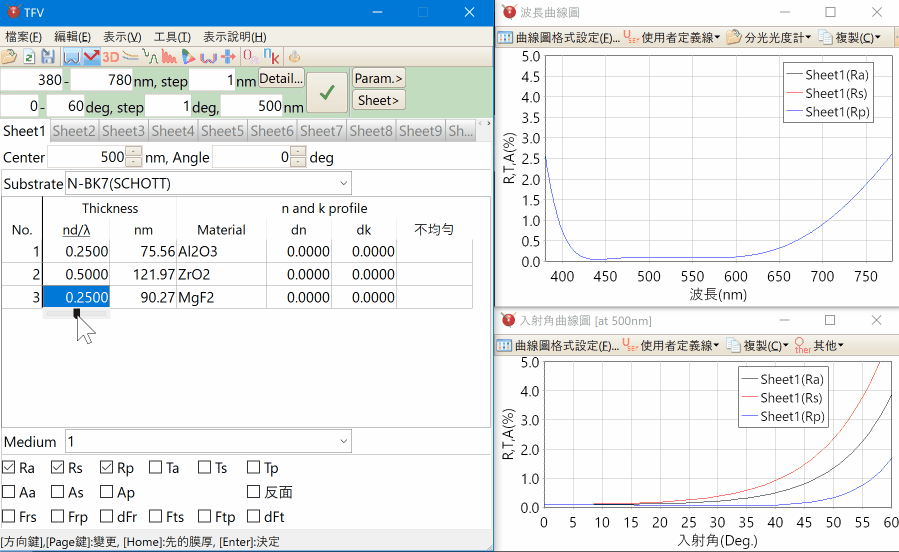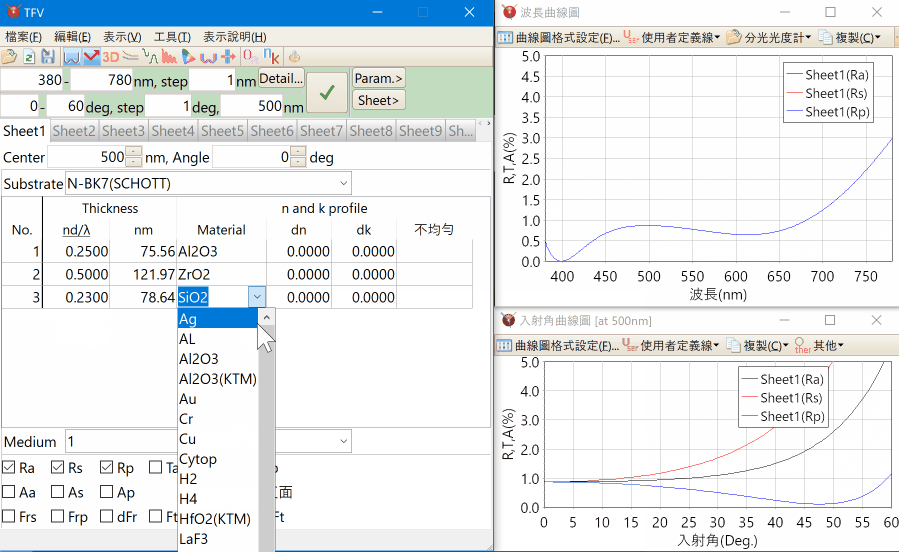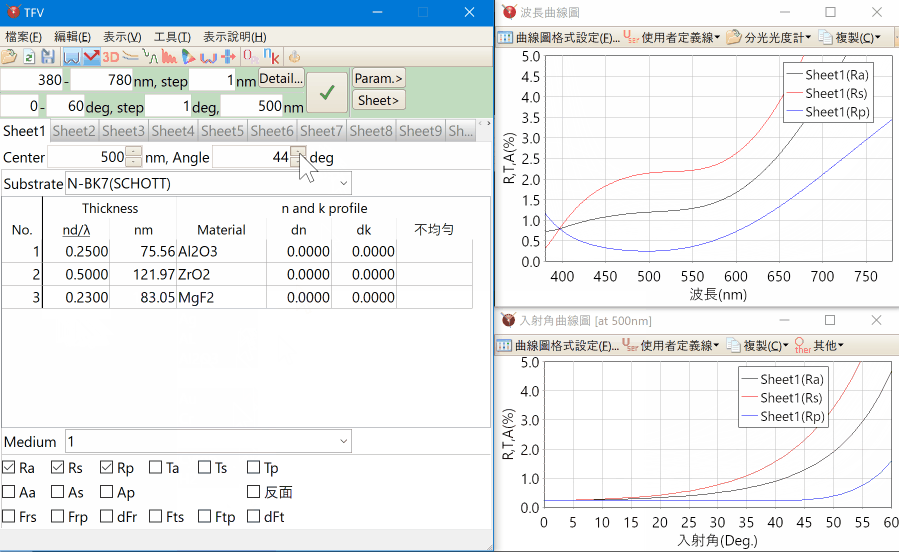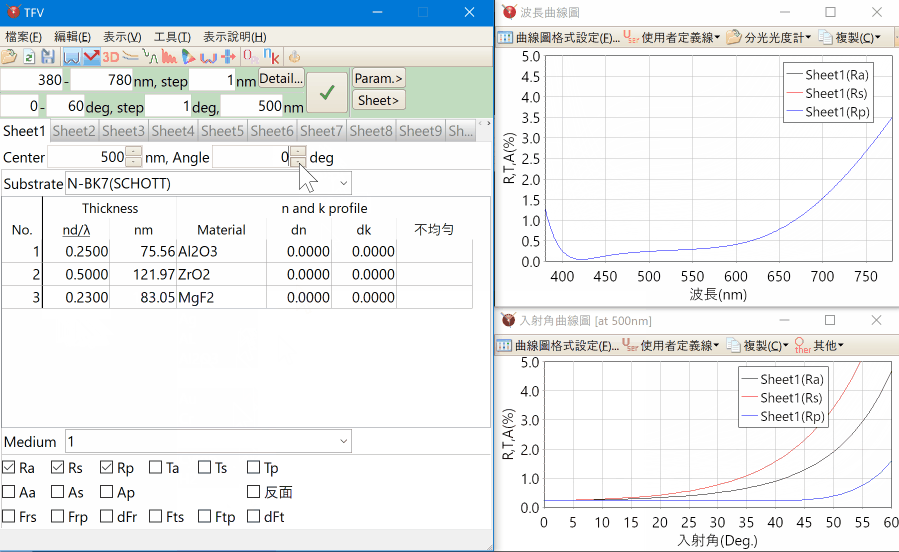
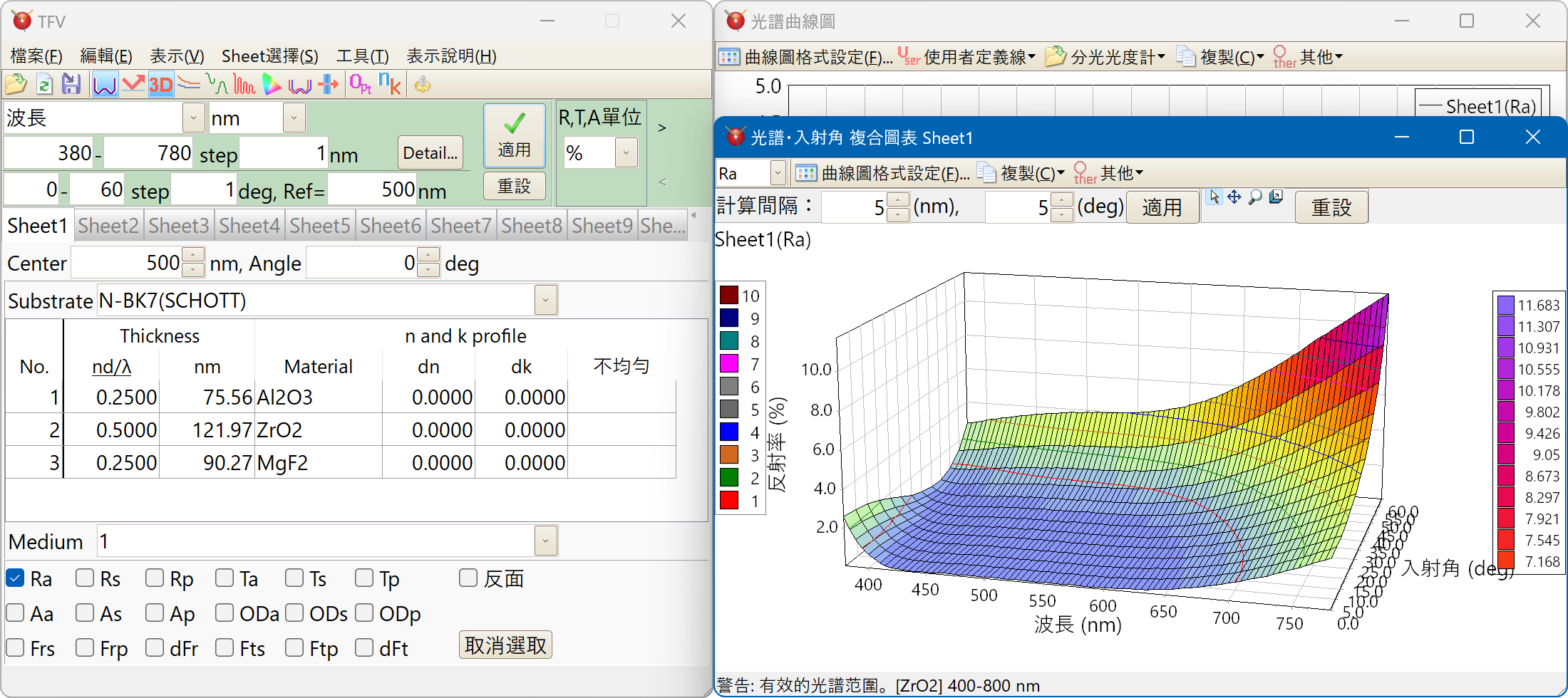
光譜、入射角的3D圖表顯示

等高線顯示。回轉、zoom可以。

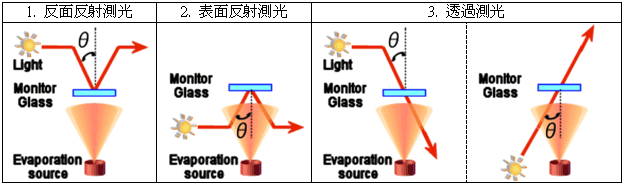
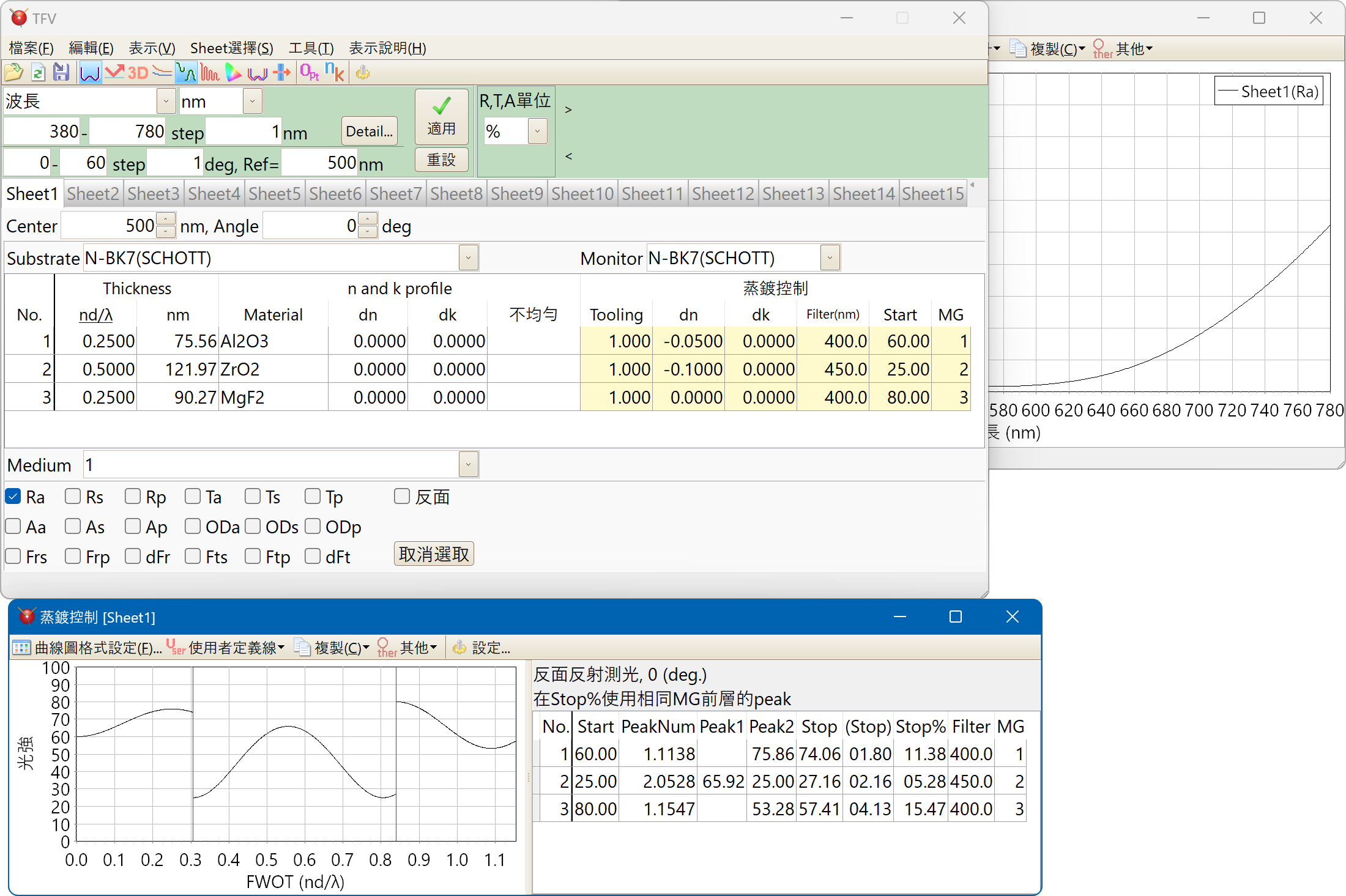
光學式蒸鍍監控

通常監控的膜厚和製品基板的膜厚會不同，且設計上的折射率(大氣中)和成膜中(真空中)的折射率也不一樣。而TFV軟體則能考慮上述問題進行模擬。

光學測光方式

電場強度分布

可選擇欲顯示的偏振光種類。

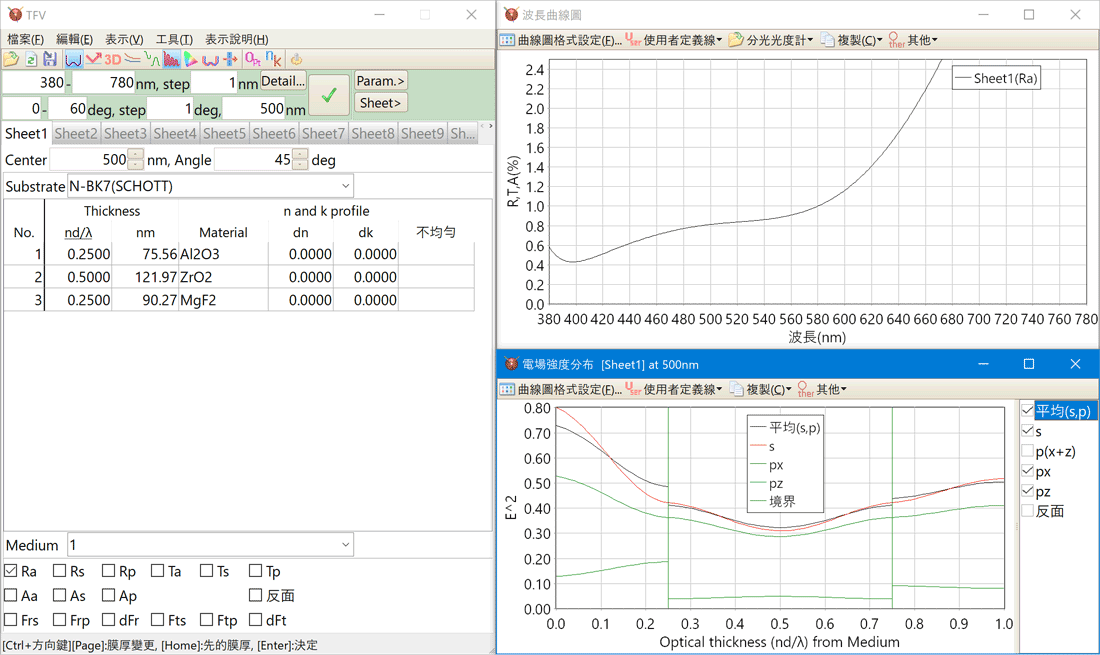
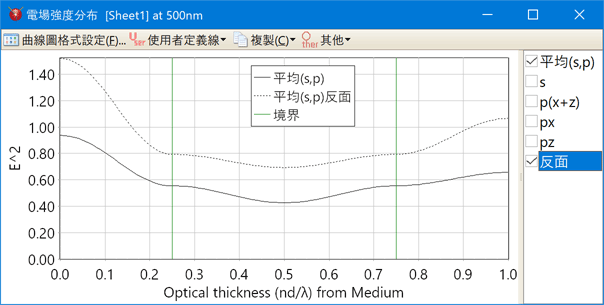
根據選擇「反面」，由表面側的入射光與反面測的入射光電場強度將可同時顯示。

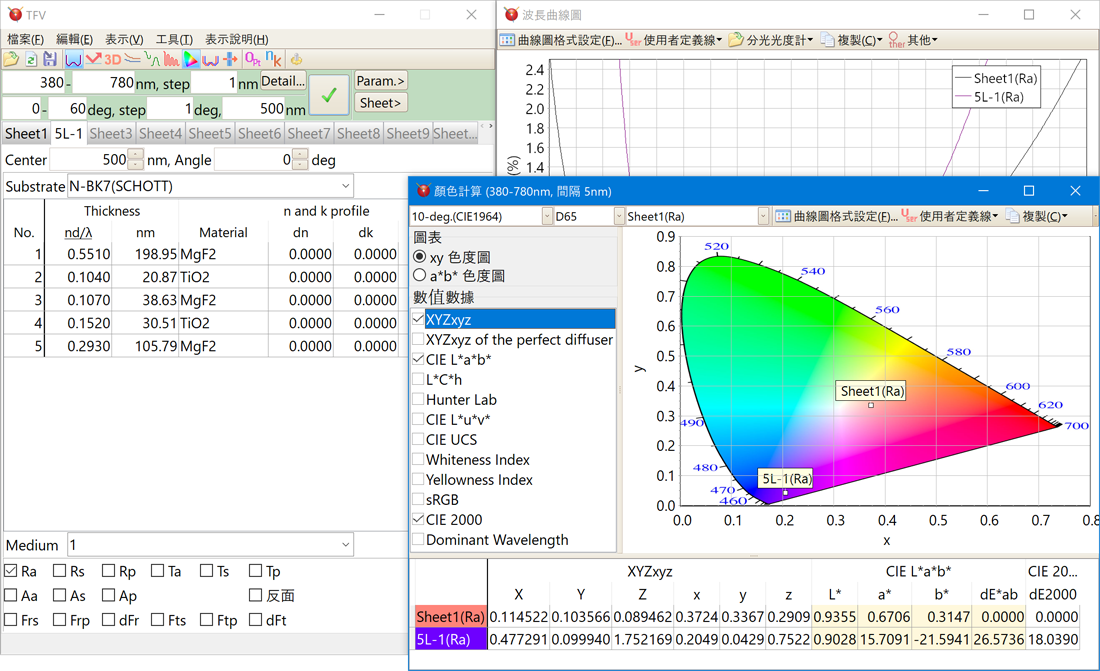
顏色計算

顯示所有工作表的計算結果，因此能夠計算各膜資料之間的色差。

表色系統: XYZxy, CIE L*a*b*, L*C*h, Hunter Lab, L*u*v*, UCS, Whiteness Index, Yellowness Index, sRGB, CIE2000, Dominant Wavelength。
對應的光源種類: A, B, C, D50, D55, D65, D75, E, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, ID50, ID65。
您也可以將自己的光源數據註冊為csv文件。

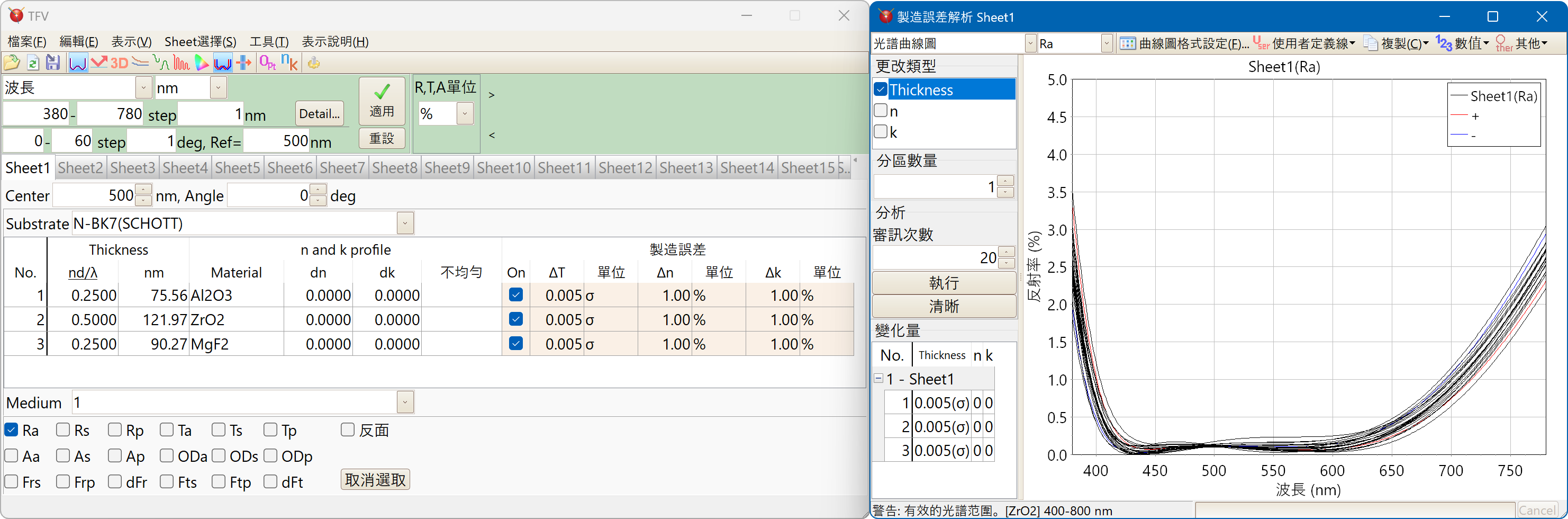
製造誤差解析

某層的膜厚、折射率、吸收係數的誤差，於調查會對光學特性會造成多少程度影響時及調查設計值與實際成形薄膜的光學特性的乖離發生在哪一層時(Mismatch解析)、及依據Monte Carlo simulation調查製造變異時(製造誤差解析)使用。

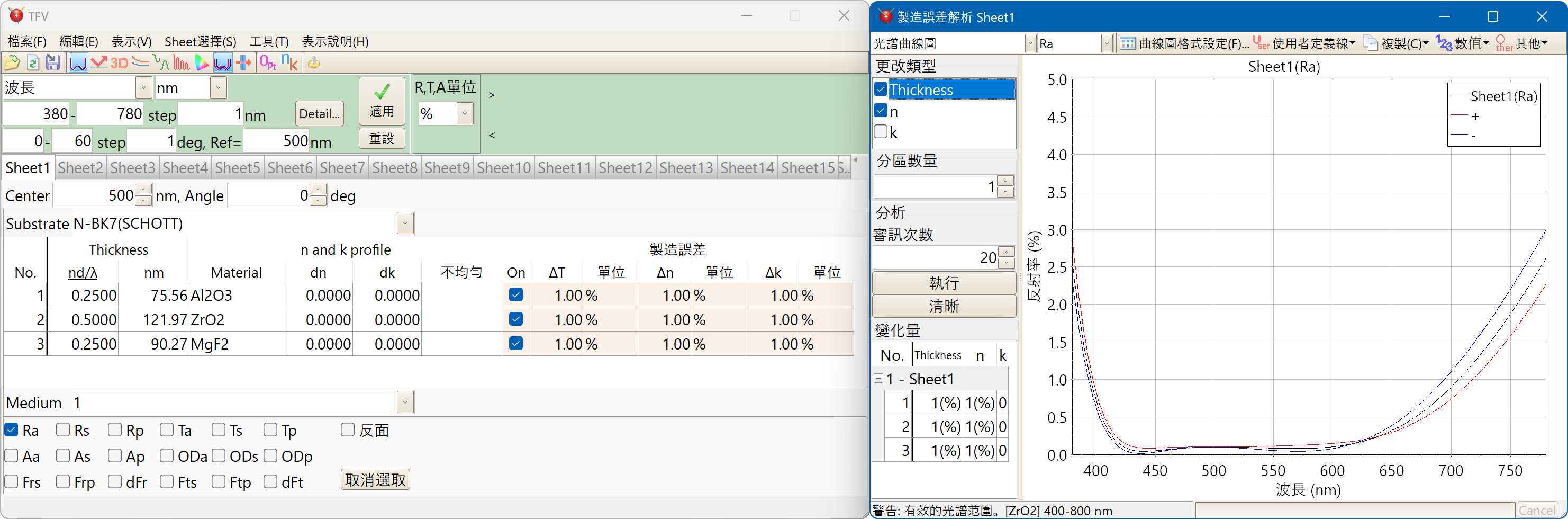
光譜曲線圖Monte Carlo simulation

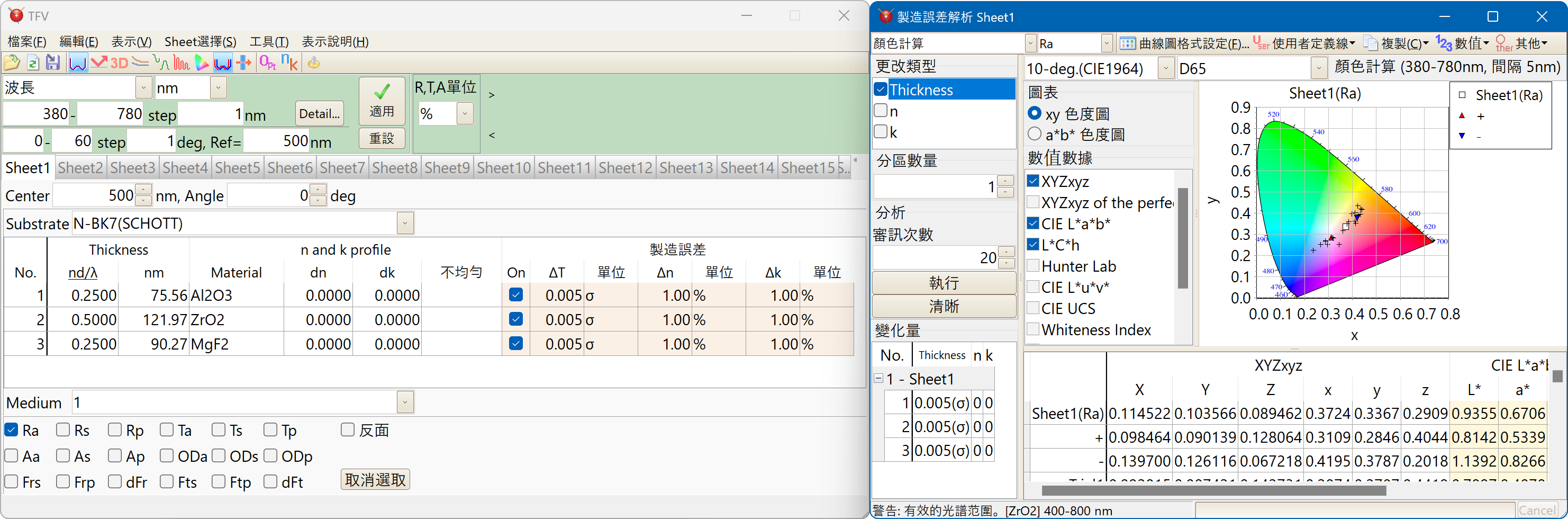
顏色計算Monte Carlo simulation

您可以為每個圖層指定每個薄膜厚度，折射率和吸收係數的變化量。
變化量可以從絕對值的均勻分佈，％的均勻分佈和正常(Gaussian)分佈(σ)中選擇。
這個軟體是用 Mersenne Twister 隨機數發生器。

群延遲

支援的群延遲種類
GD	群延遲 Group Delay
GDD	群延遲分散 Group Delay Dispersion
CDC	色散係數 Chromatic Dispersion Coefficient
TOD	三階分散 Third Order Dispersion
FOD	四階分散 Fourth Order Dispersion
5OD	五階分散 Fifth Order Dispersion

單位
ps, fs

在群延遲的計算中，微分也包含光學常數(n, k 的色散公式)。
未使用誤差較大的數值微分(差分)。

Stack(兩面的合計特性)

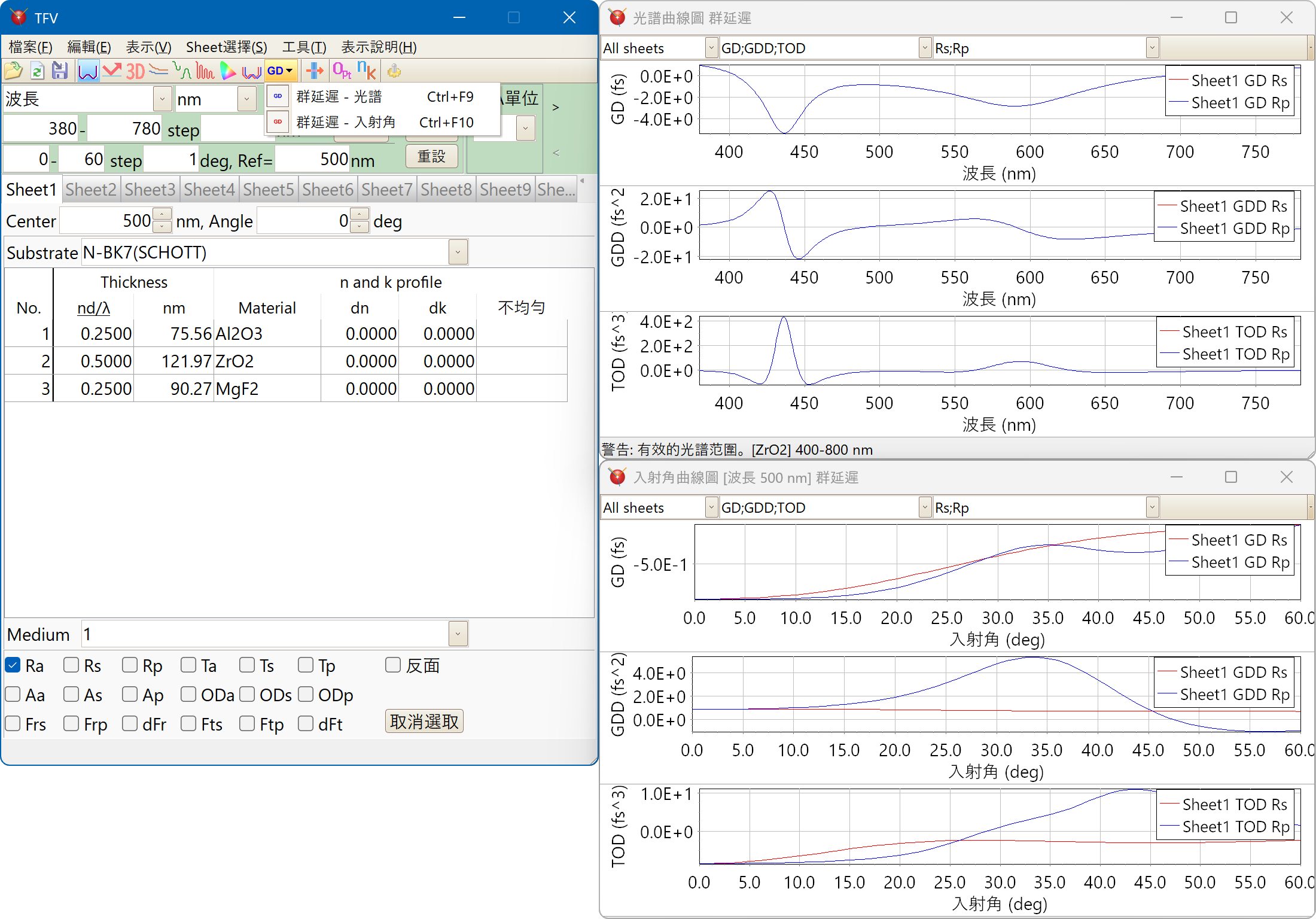
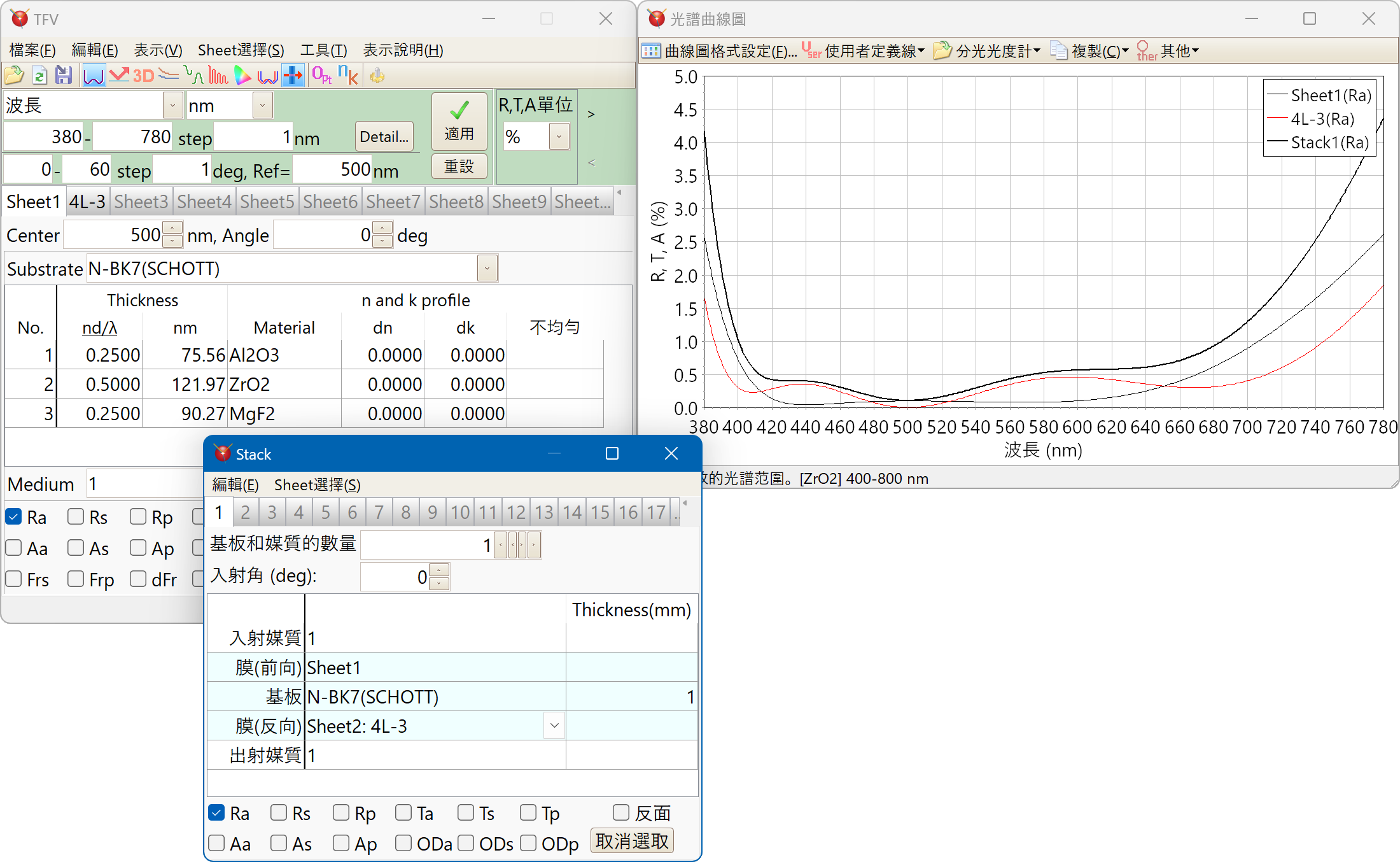
平行邊面基板的兩面(又或單面)附著於膜時的合計特性。

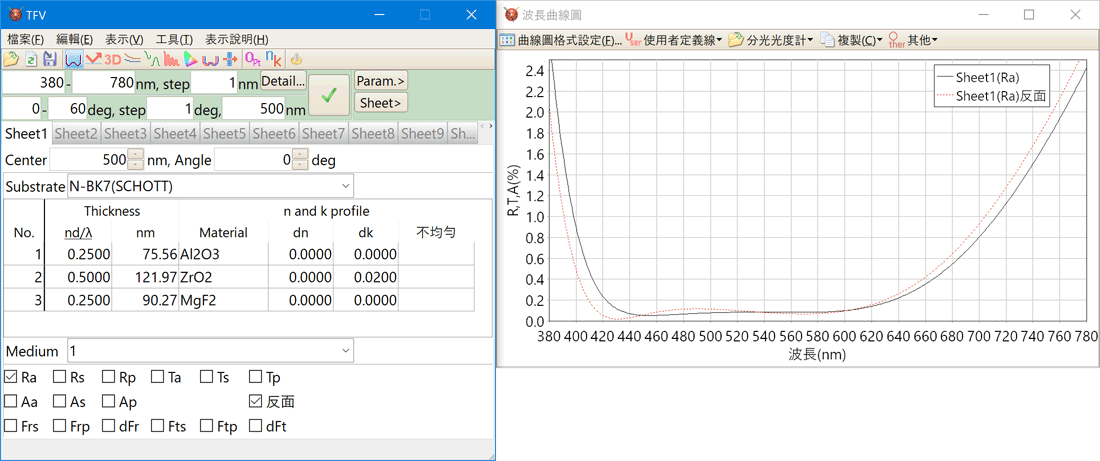
反面測的特性

可以同時觀察有吸收的膜的表面側、反面側的特性來做設計。

不均勻

不均勻(折射率斜面)設定
將游標放置在不均質的欄位上，將會跳出不均勻數據資料。

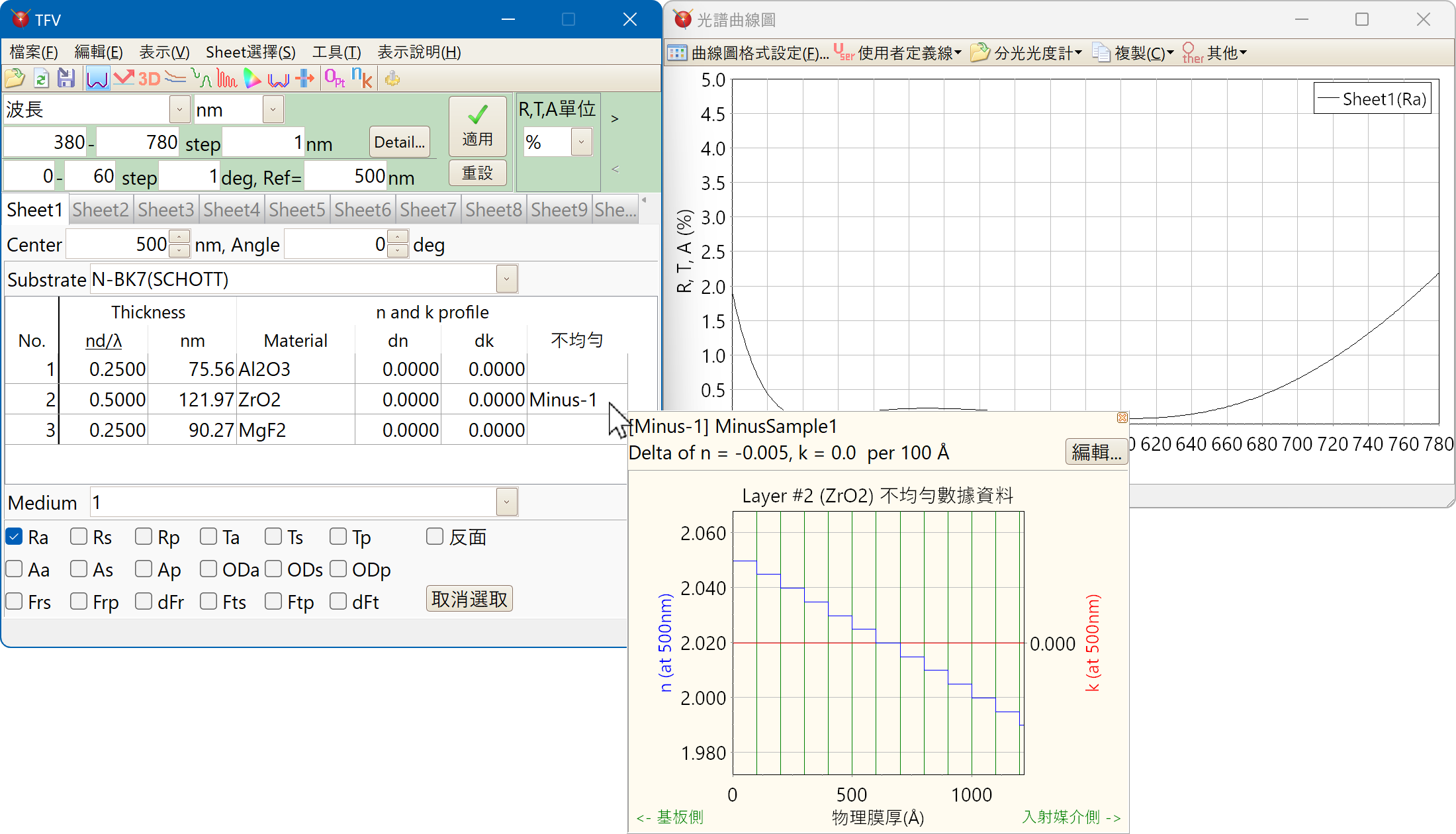
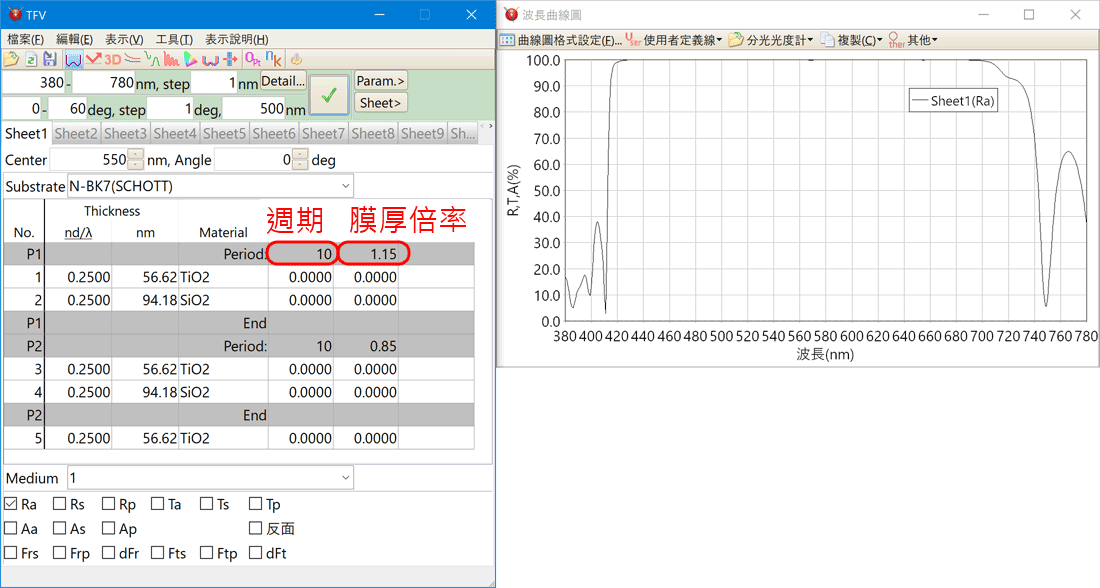
周期層

可設定週期層內的膜厚倍率。

設計最適化

設計最適化 - 標準MODE -

由Local search、Global search、Needle search三種最適化手法中選取實行最適化。

Local search: 使用Levenberg-Marquardt法，藉著邊變更膜厚邊找尋最適當解析。
Global search: Simulated Annealing Method法與Levenberg-Marquardt法組合的手法，在local search的途中，將膜厚隨意變更､避免陷入非本來解的局部解結果。
Needle search: 插入針狀的薄層，讓多層膜成長，藉此搜尋解。
Needle層的插入→local search→needle層的插入→local search的反覆循環。

設計最適化 - 手動mode -

手動mode，用滑鼠將圖表上的特性拖曳變更形狀，使用那個能使之變形的local search進行最優化的新類型最優化方法。

計算基板及薄膜nk的功能

由分光光度計測量的光譜反射率和光譜透射率計算出基板或薄膜的nk。

計算無吸收的基板的折射率(n)
計算沒有膜的基板的折射率。
在基板上無吸收時使用。
需要是單面mat基板或雙面研磨基板。
計算具有吸收作用的基板的折射率(n)，吸收係數(k)和內部透射率(Ti)
在基板上有吸收時使用。
需要是單面mat基板或雙面研磨基板。
單層膜的nk分析
從光譜反射率和光譜透射率，通過對色散公式進行曲線擬合來分析膜的n，k和膜厚度(d)。
添加了僅分析正常色散(折射率隨波長變短而增加色散)的選項。
單層金屬薄膜的nk計算
由正面反射率和背面反射率算出金屬膜的nk。
膜必須足夠厚且透射率為零。

分光光度計測定資料

讀寫分光光度計測定資料夾，將可顯示於坡長曲線圖。既可將使用分光光度計分光光度計測定的資料與設計值放於同一曲線圖做比較。
測定值為相對值時，可變換為絕對值。

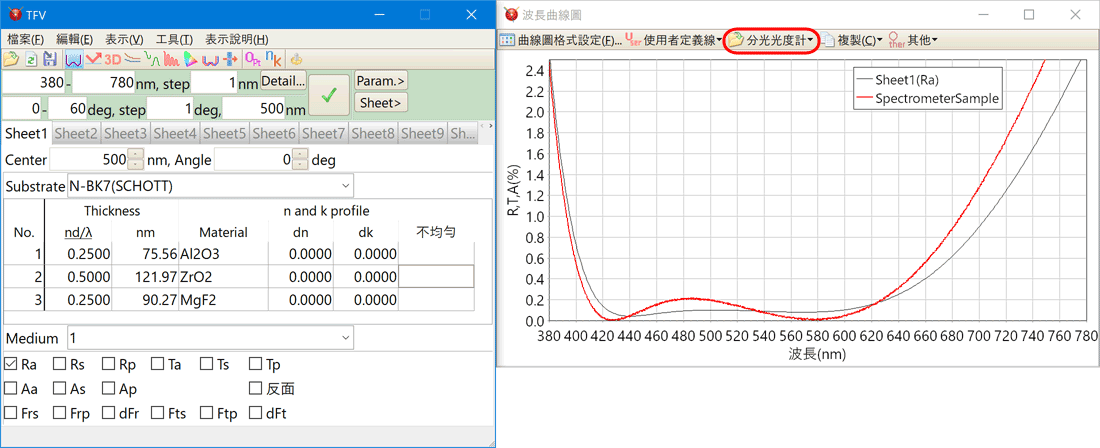
對應的檔案形式: Hitachi UV-Solutions files and UV1 files(*.UDSS, *.UDS, *.UDA),
Shimadzu SPC files,
Olympus-USPM files(*.dat, *.csv),
Jasco JWS files,
Ocean-Optics OOi-Base32 files,
csv files,
tab separated text files.

色散資料

基板data

1381基板data為事先預設。: SCHOTT, OHARA, HOYA, SUMITA, HIKARI, CDGM(成都光明)
APEL, ZEONEX, PMMA, Polycarbonate, etc.
您也可以註冊自己的數據。

膜物質data

下記膜物質data為事先預設。: Ag, Al2O3, AL, Au, Cr, Cu, H2, H4, LaF3, M3, M3-RT, MgF2, Nb2O5, Nb2O5-RT, OH5, OH5-RT, OS50, OS50-RT, SiO2, Ta2O5, Ta2O5-RT, Ti, TiO2, Zn, ZnS, ZrO2, Cytop; Al2O3(KTM), HfO2(KTM), LaF3(KTM), Ti3O5(KTM), ZrO2(KTM), ZRT2(KTM)
KTM: Kyoto Thin-Film Materials Institute; 您也可以註冊自己的數據。

色散式的種類

折射率n的色散式

Sellmeier
$n (λ) = \sqrt{1 + \frac{A_{0} λ^{2}}{λ^{2} - A_{3}} + \frac{A_{1} λ^{2}}{λ^{2} - A_{4}} + \frac{A_{2} λ^{2}}{λ^{2} - A_{5}}}$
Sellmeier2
$n (λ) = \sqrt{1 + A_{0} + \frac{A_{1} λ^{2}}{λ^{2} - {A_{3}}^{2}} + \frac{A_{2}}{λ^{2} - {A_{4}}^{2}}}$
※ A₂沒有λ²。
Sellmeier3
$n (λ) = \sqrt{1 + \frac{A_{0} λ^{2}}{λ^{2} - A_{4}} + \frac{A_{1} λ^{2}}{λ^{2} - A_{5}} + \frac{A_{2} λ^{2}}{λ^{2} - A_{6}} + \frac{A_{3} λ^{2}}{λ^{2} - A_{7}}}$
Sellmeier4
$n (λ) = \sqrt{A_{0} + \frac{A_{1} λ^{2}}{λ^{2} - A_{3}} + \frac{A_{2} λ^{2}}{λ^{2} - A_{4}}}$
Sellmeier5
$n (λ) = \sqrt{1 + \frac{A_{0} λ^{2}}{λ^{2} - A_{5}} + \frac{A_{1} λ^{2}}{λ^{2} - A_{6}} + \frac{A_{2} λ^{2}}{λ^{2} - A_{7}} + \frac{A_{3} λ^{2}}{λ^{2} - A_{8}} + \frac{A_{4} λ^{2}}{λ^{2} - A_{9}}}$
SellmeierT1
$n (λ) = \sqrt{A_{0} + \frac{A_{1} λ^{2}}{λ^{2} - A_{2}}}$
SellmeierT2
$n (λ) = \sqrt{A_{0} + \frac{A_{1} λ^{2}}{λ^{2} - A_{2}} + A_{3} λ^{2}}$
SellmeierX1
$n (λ) = \sqrt{1 + \frac{A_{0} λ^{2}}{λ^{2} - {A_{3}}^{2}} + \frac{A_{1} λ^{2}}{λ^{2} - {A_{4}}^{2}} + \frac{A_{2} λ^{2}}{λ^{2} - {A_{5}}^{2}}}$
General1
$n (λ) = \sqrt{A_{0} + A_{1} λ^{2} + \frac{A_{2}}{λ^{2}} + \frac{A_{3}}{λ^{4}} + \frac{A_{4}}{λ^{6}} + \frac{A_{5}}{λ^{8}} + A_{6} λ^{4}}$
General2 (Old Schott)
$n (λ) = \sqrt{A_{0} + A_{1} λ^{2} + \frac{A_{2}}{λ^{2}} + \frac{A_{3}}{λ^{4}} + \frac{A_{4}}{λ^{6}} + \frac{A_{5}}{λ^{8}}}$
Cauchy
$n (λ) = A_{0} + \frac{A_{1}}{λ^{2}} + \frac{A_{2}}{λ^{4}}$
Hartmann1
$n (λ) = A_{0} + \frac{A_{1}}{λ - A_{2}}$
Hartmann2
$n (λ) = A_{0} + \frac{A_{1}}{(λ - A_{2})^{2}}$
Herzberger
$n (λ) = A_{0} + A_{1} λ^{2} + \frac{A_{2}}{(λ^{2} - {0.168}^{2})} + \frac{A_{3}}{(λ^{2} - {0.168}^{2})^{2}}$
Herzberger2
$n (λ) = A_{0} + \frac{A_{1}}{(λ^{2} - 0.028)} + \frac{A_{2}}{(λ^{2} - 0.028)^{2}} + A_{3} λ^{2} + A_{4} λ^{4} + A_{5} λ^{6}$
QUAD
$n (λ) = A_{0} + \frac{A_{1}}{λ^{2}}$
QUADSK
$n (λ) = A_{0} + A_{1} λ + A_{2} λ^{2}$
Conrady
$n (λ) = A_{0} + \frac{A_{1}}{λ} + \frac{A_{2}}{λ^{3.5}}$
Handbook1 (Handbook of Optics)
$n (λ) = \sqrt{A_{0} + \frac{A_{1}}{(λ^{2} - A_{2})} - A_{3} λ^{2}}$
Handbook2 (Handbook of Optics)
$n (λ) = \sqrt{A_{0} + \frac{A_{1} λ^{2}}{(λ^{2} - A_{2})} - A_{3} λ^{2}}$
Extended (ZEMAX)
$n (λ) = \sqrt{A_{0} + A_{1} λ^{2} + \frac{A_{2}}{λ^{2}} + \frac{A_{3}}{λ^{4}} + \frac{A_{4}}{λ^{6}} + \frac{A_{5}}{λ^{8}} + \frac{A_{6}}{λ^{10}} + \frac{A_{7}}{λ^{12}}}$
Extended2 (ZEMAX)
$n (λ) = \sqrt{A_{0} + A_{1} λ^{2} + \frac{A_{2}}{λ^{2}} + \frac{A_{3}}{λ^{4}} + \frac{A_{4}}{λ^{6}} + \frac{A_{5}}{λ^{8}} + A_{6} λ^{4} + A_{7} λ^{6}}$
Extended3 (ZEMAX)
$n (λ) = \sqrt{A_{0} + A_{1} λ^{2} + A_{2} λ^{4} + \frac{A_{3}}{λ^{2}} + \frac{A_{4}}{λ^{4}} + \frac{A_{5}}{λ^{6}} + \frac{A_{6}}{λ^{8}} + \frac{A_{7}}{λ^{10}} + \frac{A_{8}}{λ^{12}}}$
Buchdahl
$n (λ) = A_{0} + A_{1} ω (λ) + A_{2} ω (λ)^{2}$ $ω (λ) = \frac{λ - A_{3}}{1 + 2.5 (λ - A_{3})}$
DRUDE
$n^{2} (λ) - k^{2} (λ) = A_{0} - \frac{A_{1} {A_{2}}^{2} λ^{2}}{λ^{2} + {A_{2}}^{2}}$
LorentzianK
$n (λ) = \sqrt{A_{0} + k^{2} (λ) + A_{1} λ^{2} \frac{(λ^{2} - {A_{2}}^{2})}{(λ^{2} - {A_{2}}^{2})^{2} + {A_{3}}^{2} λ^{2}}}$
Forouhi-Bloomer
$n (E) = n (\infty) + \frac{B_{0} E + C_{0}}{E^{2} - B E + C}$ $B_{0} = \frac{A}{Q} (\frac{- B^{2}}{2} + E_{g} B - {E_{g}}^{2} + C)$ $C_{0} = \frac{A}{Q} (({E_{g}}^{2} + C) \frac{B}{2} - 2 E_{g} C)$ $Q = \frac{1}{2} {(4 C - B^{2})}^{\frac{1}{2}}$ $E = \frac{h c}{λ}$
h: 普朗克常數, c: 光速, E的單位是eV
n(∞), Eg, A, B, C: 材料原有的參數(色散公式係數)
A₀, A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉為物質決定的定數。
λ的單位為μm (不包括Forouhi-Bloomer)。

吸收係數k的色散式

Sellmeier
$k (λ) = {[n (λ) (B_{0} λ + \frac{B_{1}}{λ} + \frac{B_{2}}{λ^{3}})]}^{- 1}$
Cauchy
$k (λ) = B_{0} + \frac{B_{1}}{λ^{2}} + \frac{B_{2}}{λ^{4}}$
Exponential
$k (λ) = B_{0} \cdot e x p (B_{1} λ^{- 1})$
QUADSK
$k (λ) = B_{0} + B_{1} λ + B_{2} λ^{2}$
DRUDE
$2 n (λ) k (λ) = \frac{A_{1} A_{2} λ^{3}}{λ^{2} + {A_{2}}^{2}}$
LorentzianK
$k (λ) = \sqrt{\frac{0.5}{n (λ)} \cdot \frac{A_{1} A_{3} λ^{3}}{(λ^{2} - {A_{2}}^{2})^{2} + {A_{3}}^{2} λ^{2}}}$
Forouhi-Bloomer
$k (E) = \frac{A (E - E_{g})^{2}}{E^{2} - B E + C}$ $E = \frac{h c}{λ}$
h: 普朗克常數, c: 光速, E的單位是eV
Eg, A, B, C: 材料原有的參數(色散公式係數)
B₀, B₁, B₂為物質決定的定數。
λ的單位為μm (不包括Forouhi-Bloomer)。

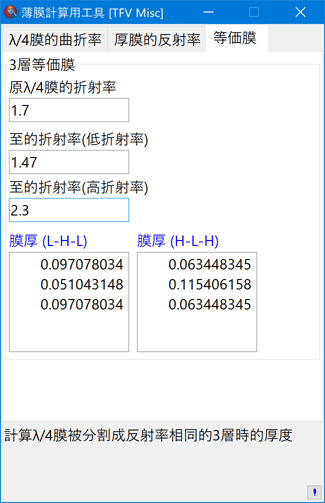
薄膜計算工具

附有簡易計算關於薄膜的「薄膜計算工具」。

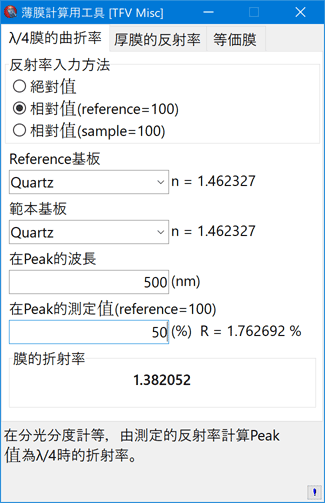
λ/4膜的折射率

由單層膜的反射率測定Peek值來計算折射率的功能率。

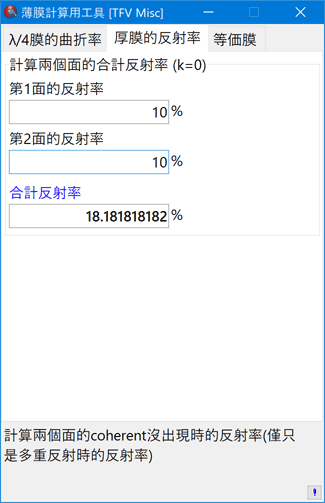
厚膜的反射率

計算兩個面的合計反射率功能。

3層等価膜

將某折射率的λ/4膜，移至另2種折射率的3層膜裡，呈現與反射率相同一般的功能。作為實際的膜材料，欲將不存在的折射率λ/4膜與已存在的兩種類膜材料做交換時膜使用。

變更日誌

選單

首頁
功能介紹
變更日誌
下載
聯絡、常問問題
僅限客戶
簡單的薄膜計算工具
最新消息