機能紹介
基本操作
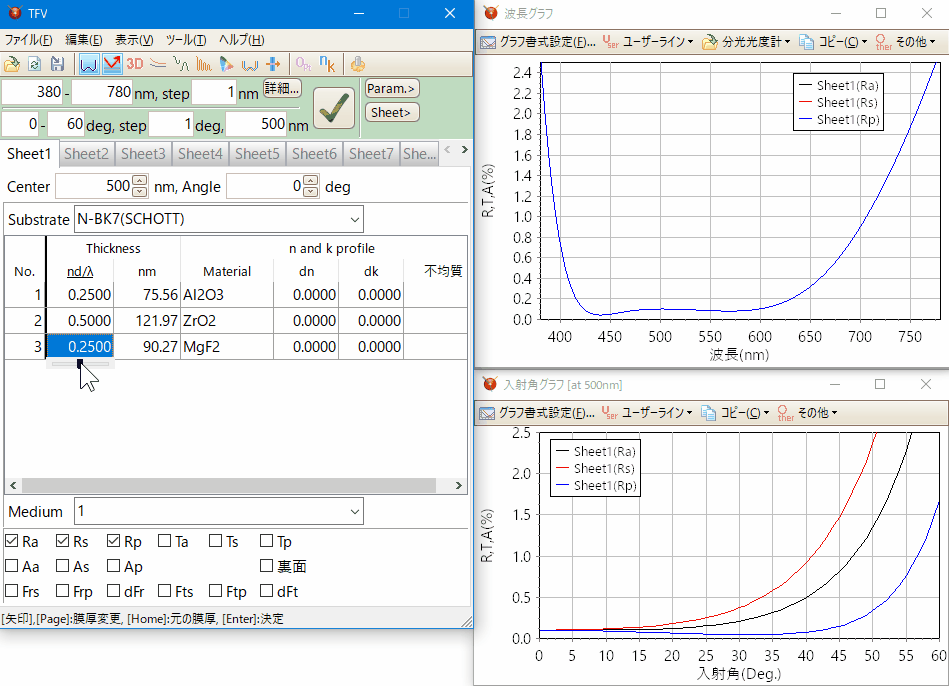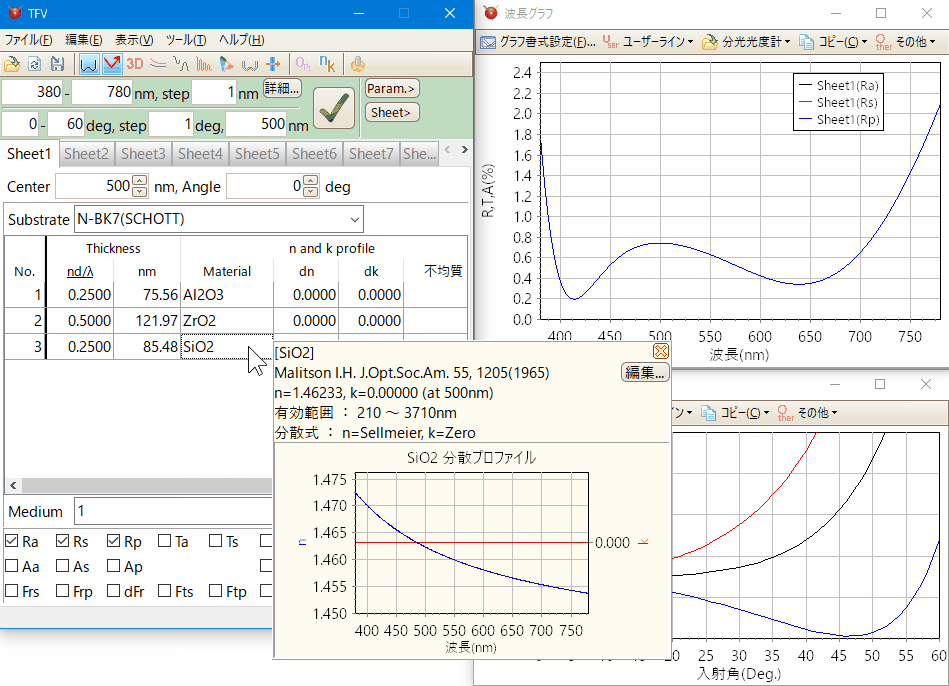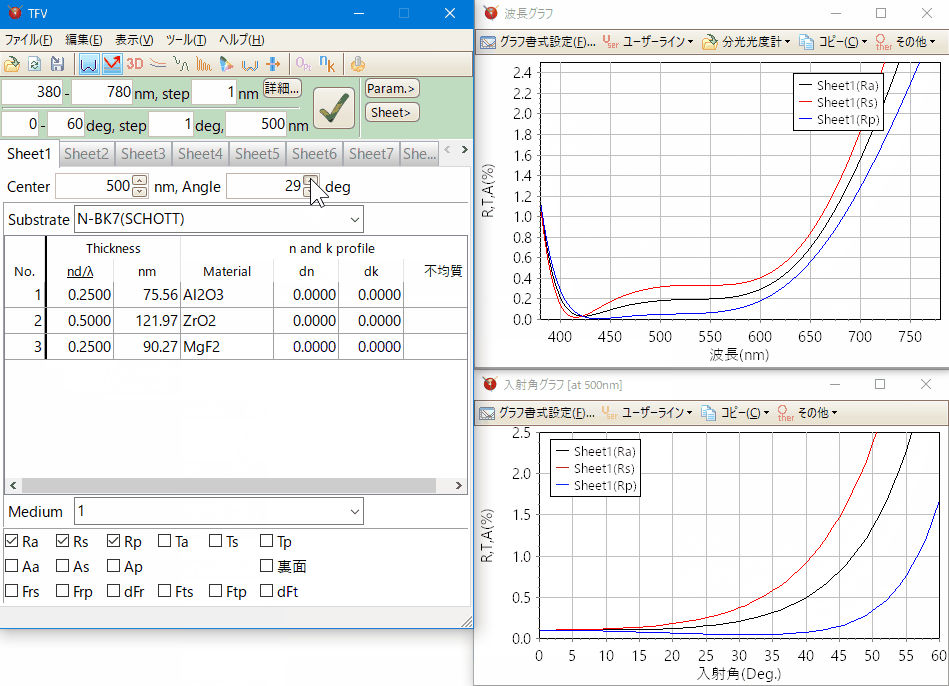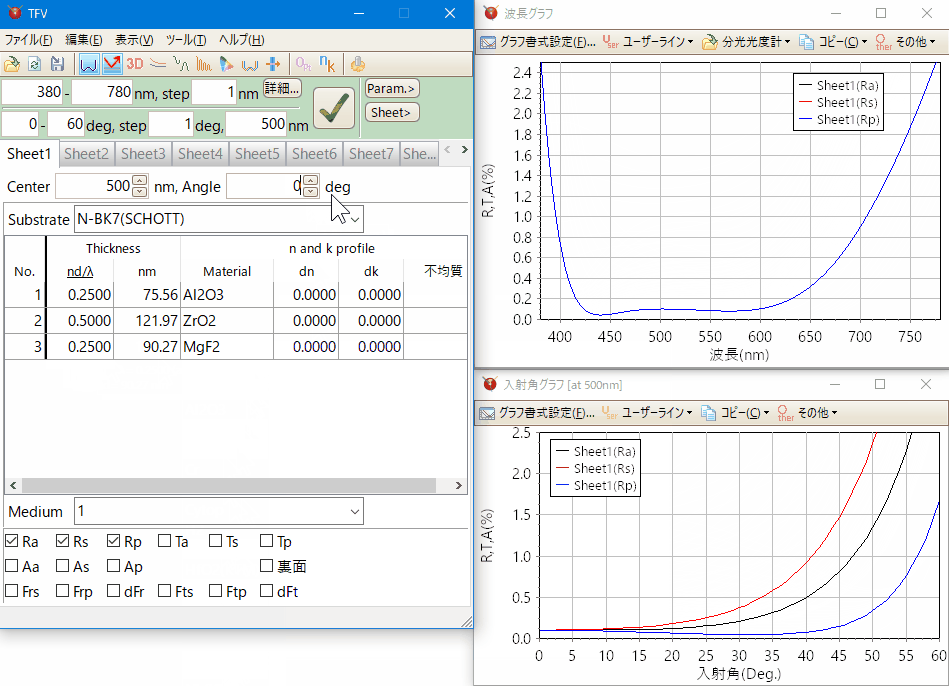
スライドバーやアップダウンボタンによるマウス操作で、膜厚や膜物質が素早く変更でき、変更は即座にグラフに反映されます。
スペクトルグラフ・入射角グラフ等、各種のグラフを同時に表示させながら設計できます。
タブ型シートにより、最大20個の設計データーをグラフに重ね書きできます。
3Dグラフ
波長などのスペクトルと入射角をxy軸にした3Dグラフを表示できます。
等高線を任意に設定して表示することができます。
マウスによる回転・拡大縮小も可能です。
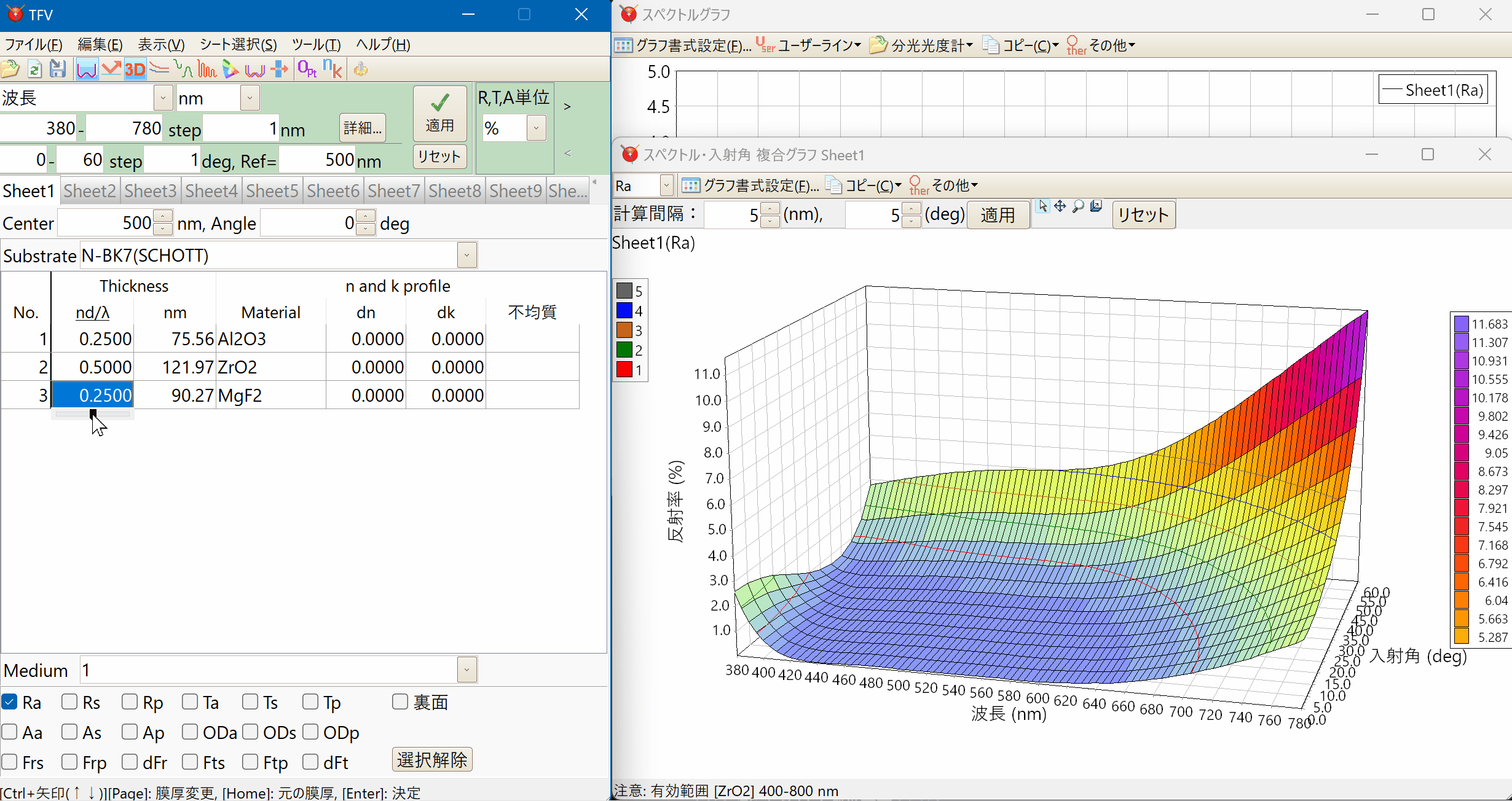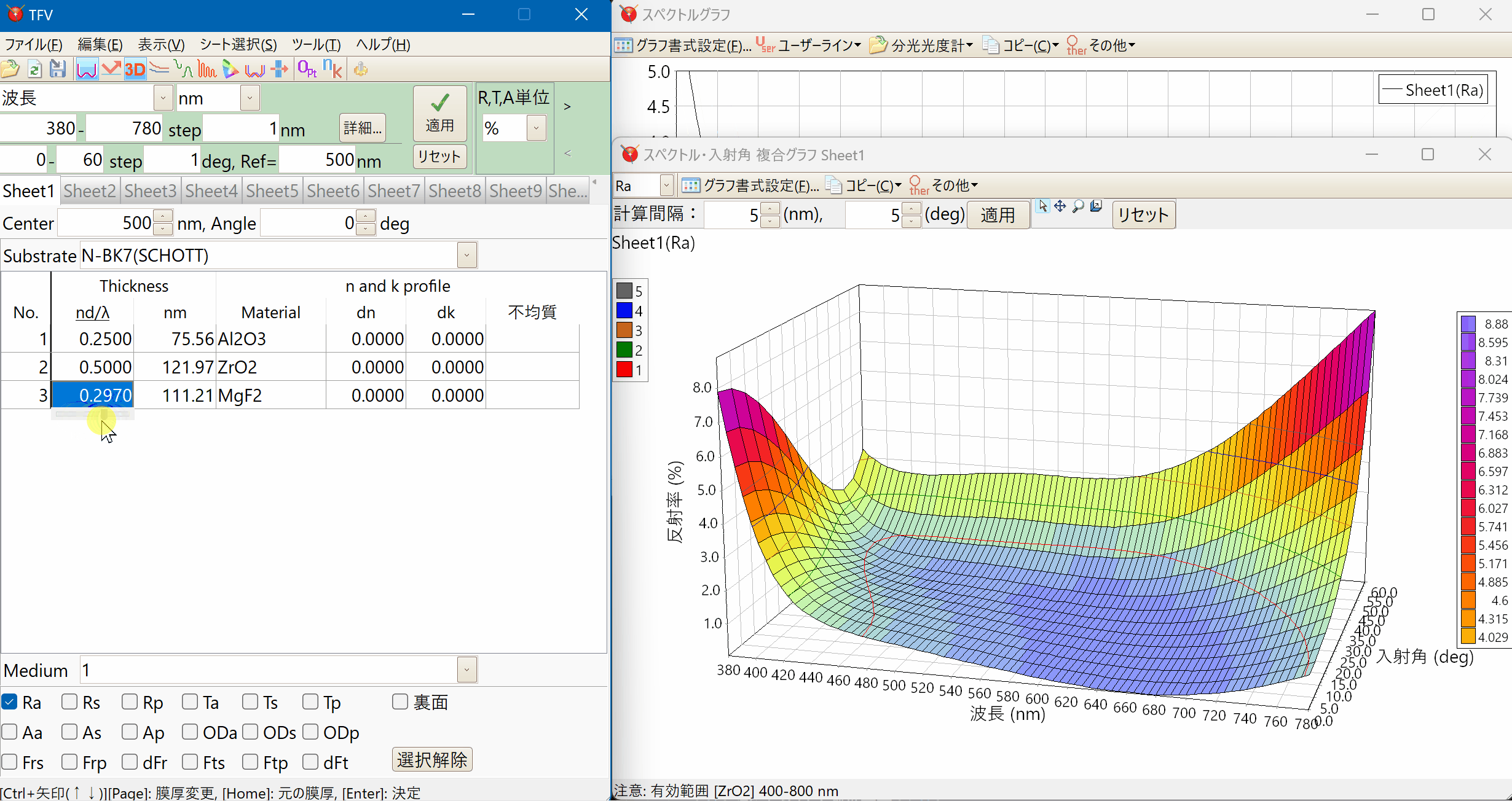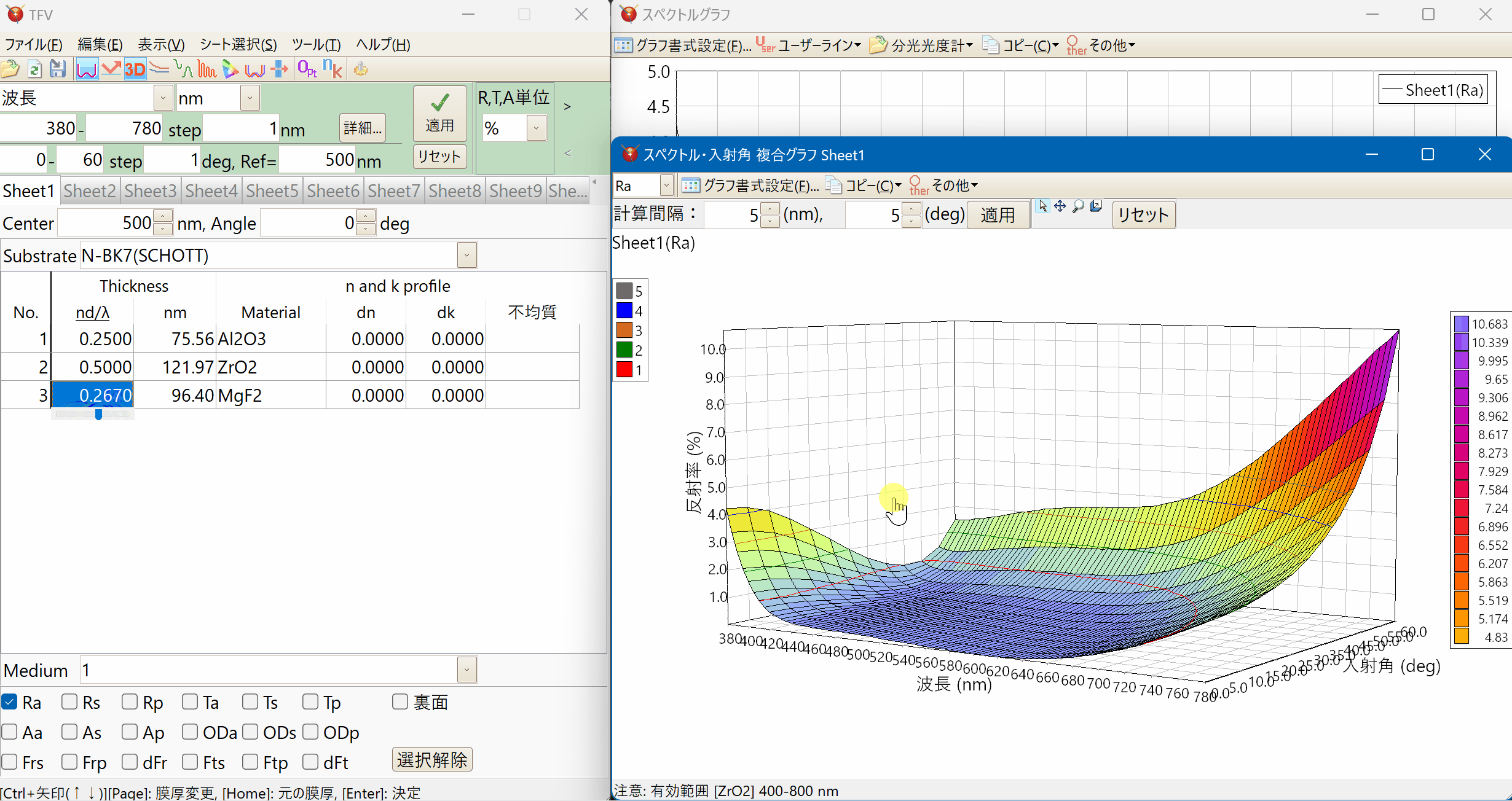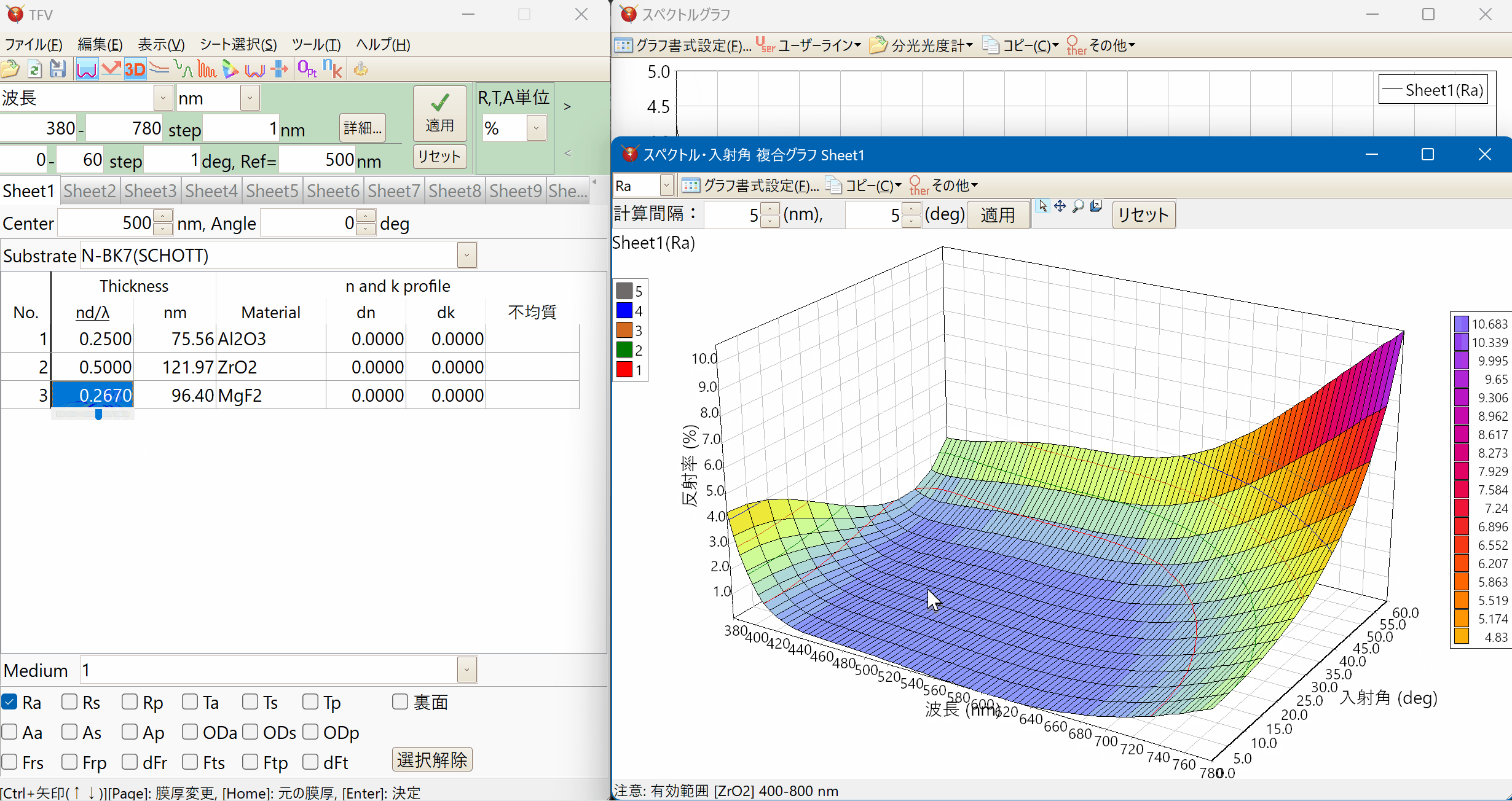
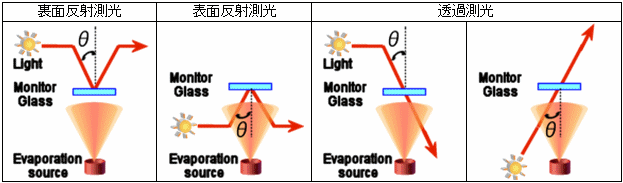
光学式蒸着モニター
モニターガラス上の膜厚と製品基板上の膜厚の差(Tooling)、設計上の屈折率・吸収係数(大気中)と成膜中(真空中)の屈折率・吸収係数の差を考慮したシミュレーションが可能です。
成膜レート、ガス導入条件、イオンビーム条件などによる光量ピークの変動への対応が容易におこなえます。
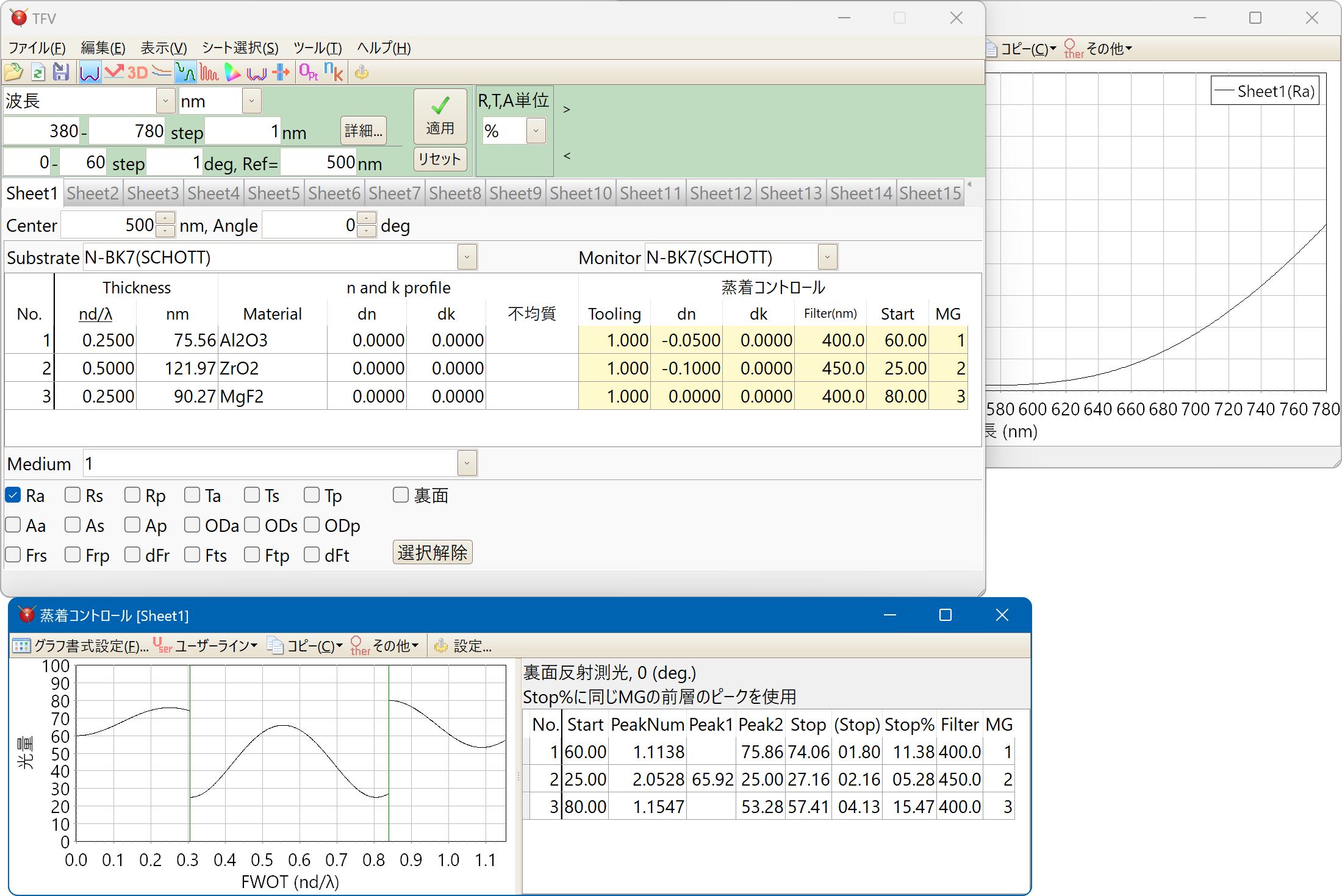
電場強度分布
偏光成分別の電場強度分布が表示できます。
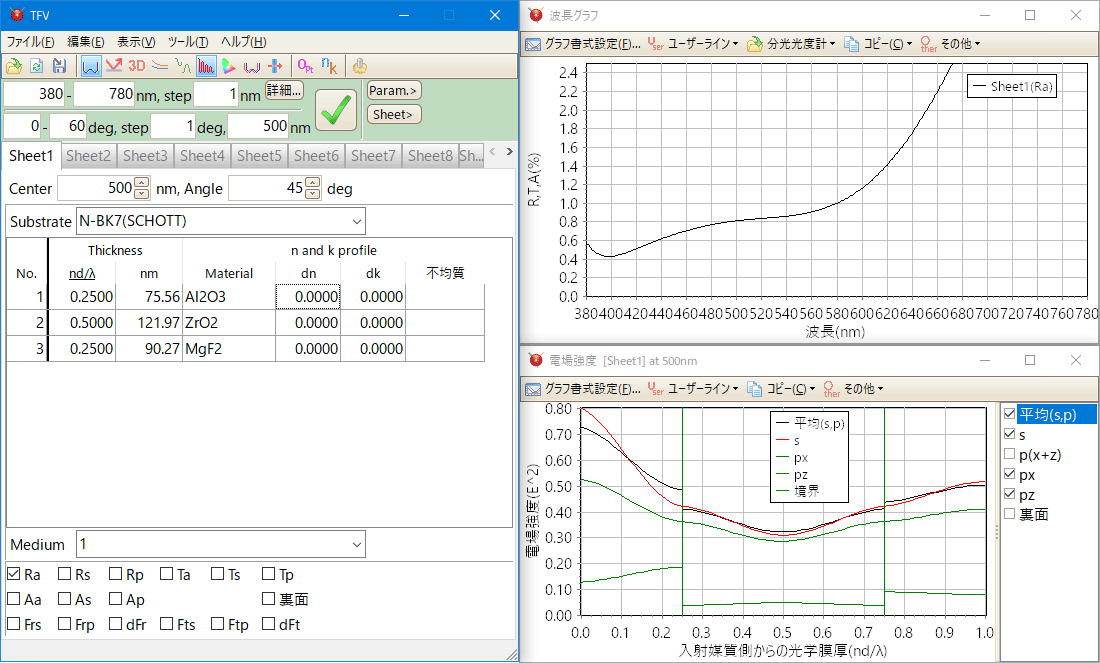
表面側からの入射光の電場強度と裏面側からの入射光の電場強度を同時に表示できます。
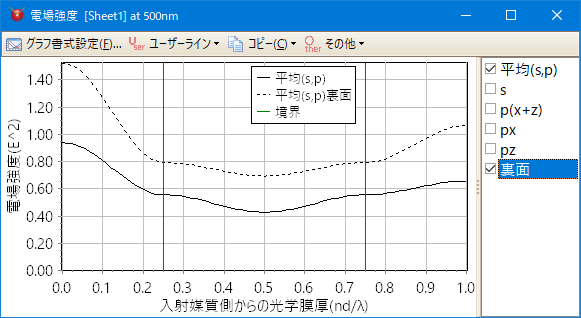
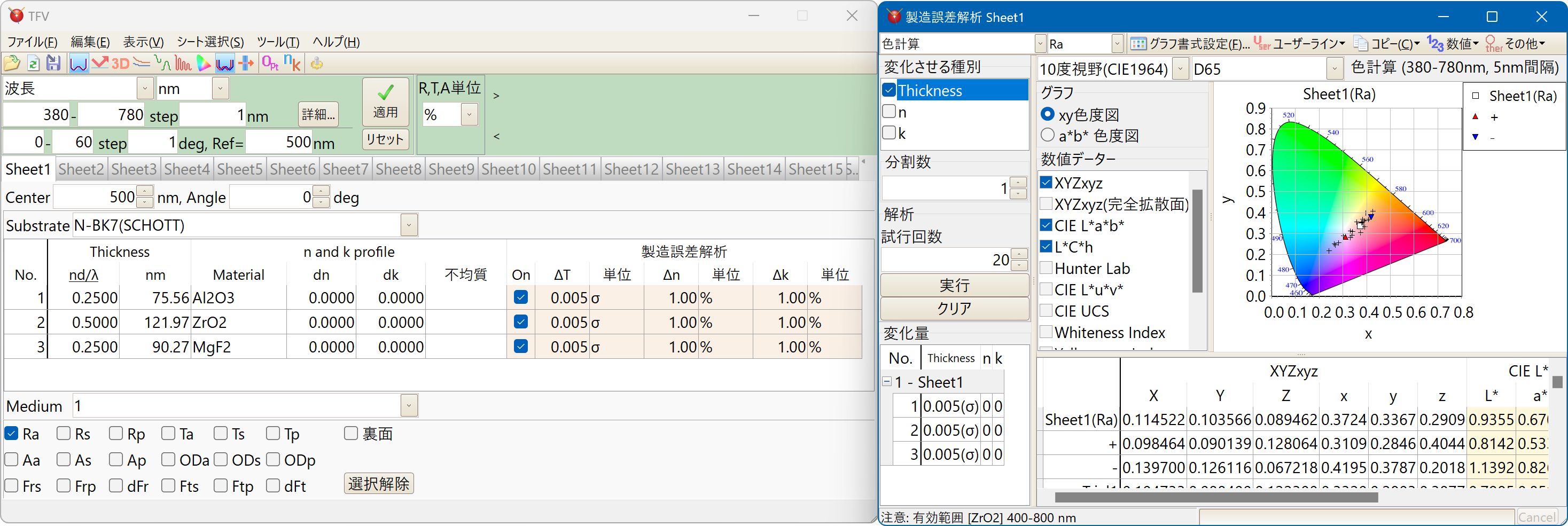
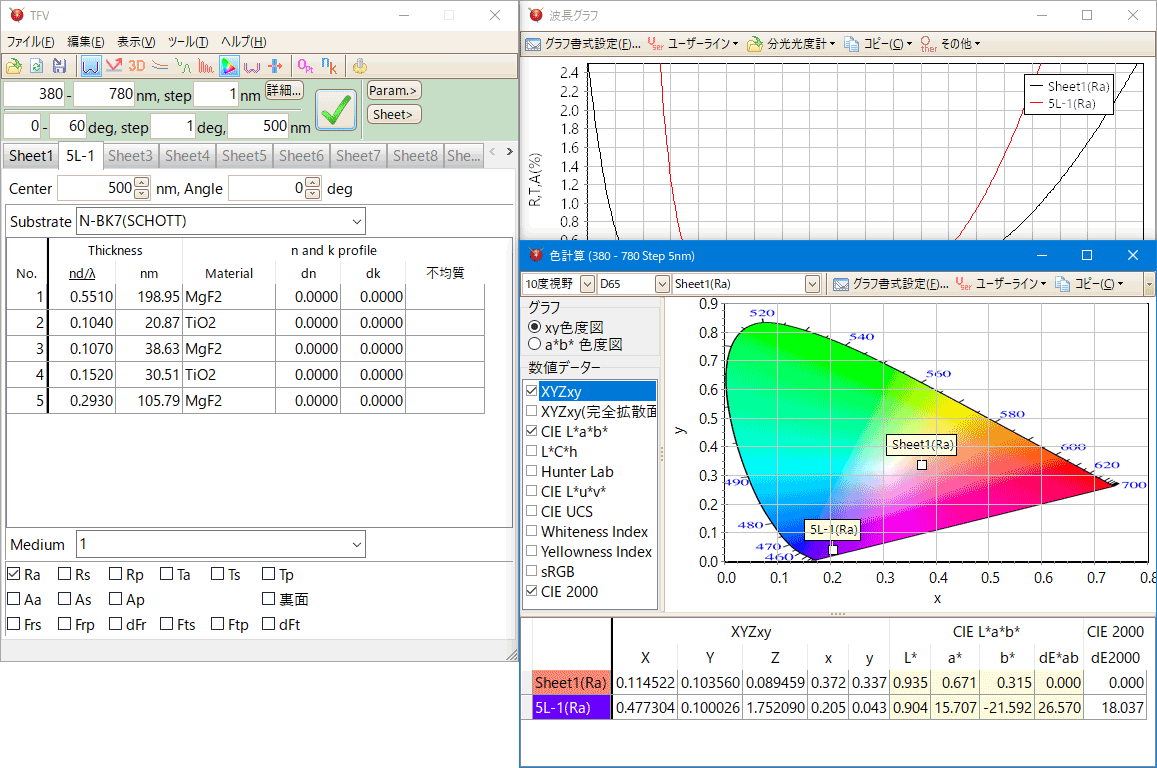
色計算
様々な種類の光源・表色系に対応しています。
2つの設計間の色差・吸収がある膜の表面と裏面の色差も計算できます。
- 対応している表色系
-
XYZxy, CIE L*a*b*, L*C*h, Hunter Lab, L*u*v*, UCS, Whiteness Index, Yellowness Index, sRGB, CIE2000, Dominant Wavelength。
- 対応している光源の種類
-
A, B, C, D50, D55, D65, D75, E, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, ID50, ID65。
お客様独自の光源データーをcsvファイルで作成して登録することもできます。
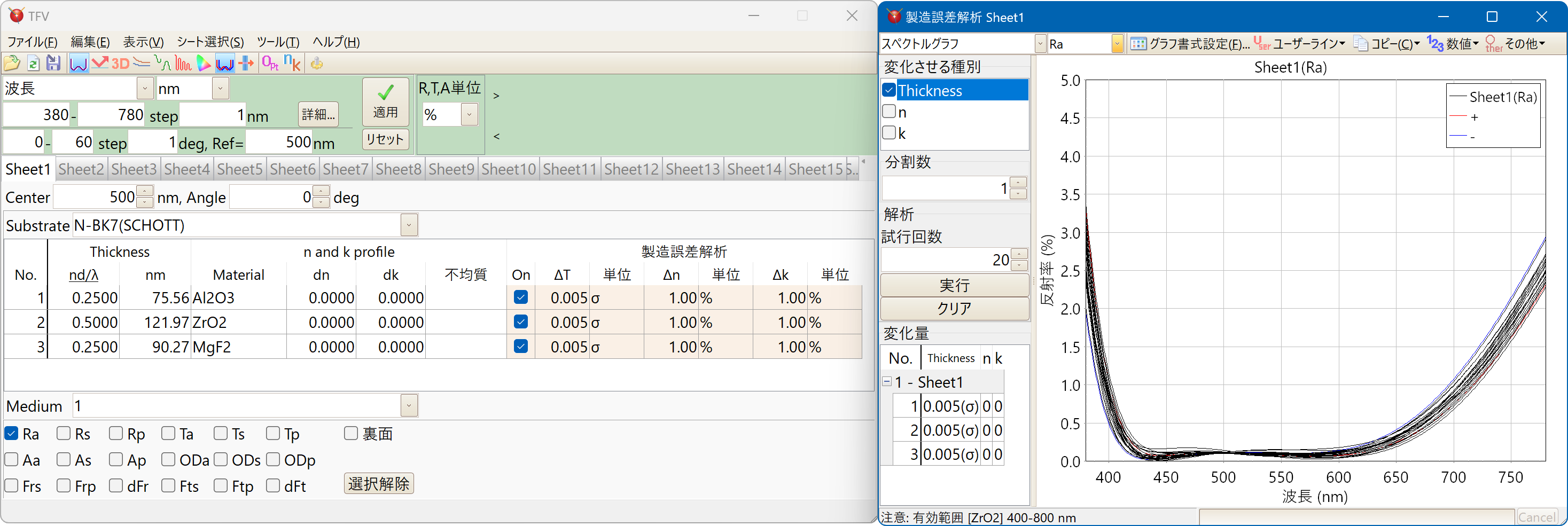
製造誤差解析
ある層の膜厚・屈折率・吸収係数の誤差が、光学特性にどの程度影響するかを調べるときや、設計値と実際に成膜した薄膜の光学特性との乖離がどの層に起因しているのかを調べるときなどに使用します。
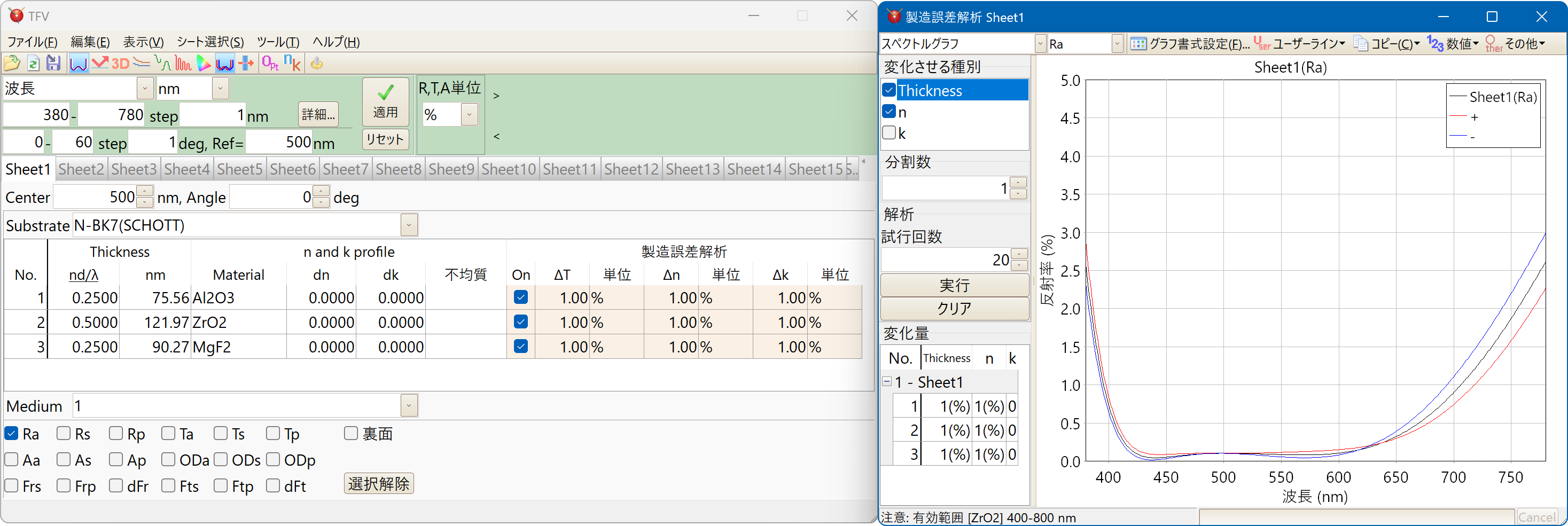
分光特性のモンテカルロシミュレーション
色のモンテカルロシミュレーション
膜厚・屈折率・吸収係数それぞれ各層毎に、絶対値での一様分布・%での一様分布・正規(ガウス)分布(σ)から選択して、変化量を指定できます。
乱数の生成には、高品質な乱数生成法として定評のあるメルセンヌ・ツイスター法(Mersenne twister)を使用しています。
群遅延
| 対応している群遅延の種類 | |
|---|---|
| GD | 群遅延 Group Delay |
| GDD | 群遅延分散 Group Delay Dispersion |
| CDC | 色分散係数 Chromatic Dispersion Coefficient |
| TOD | 3次分散 Third Order Dispersion |
| FOD | 4次分散 Fourth Order Dispersion |
| 5OD | 5次分散 Fifth Order Dispersion |
| 単位 |
|---|
| ps, fs |
光学定数(n,kの分散式)も含めて微分しています。
誤差が大きい数値微分(差分)は使用していません。

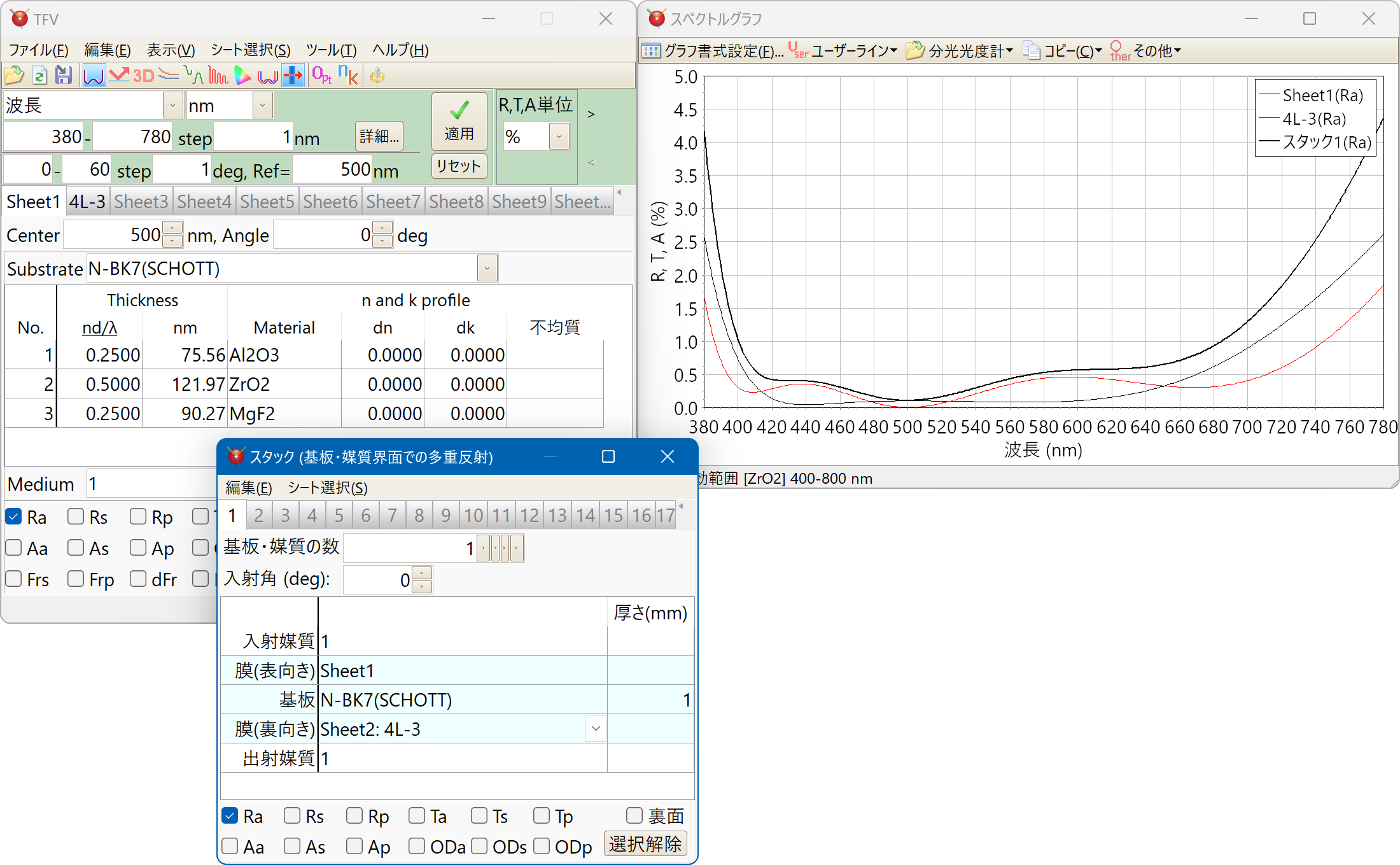
複数基板の計算(スタック)
複数の基板(平行平面基板)の各面に膜が付いた場合の合計の計算ができます。
膜の部分は光が干渉する、基板と媒質の部分は光が多重反射する、として計算します。
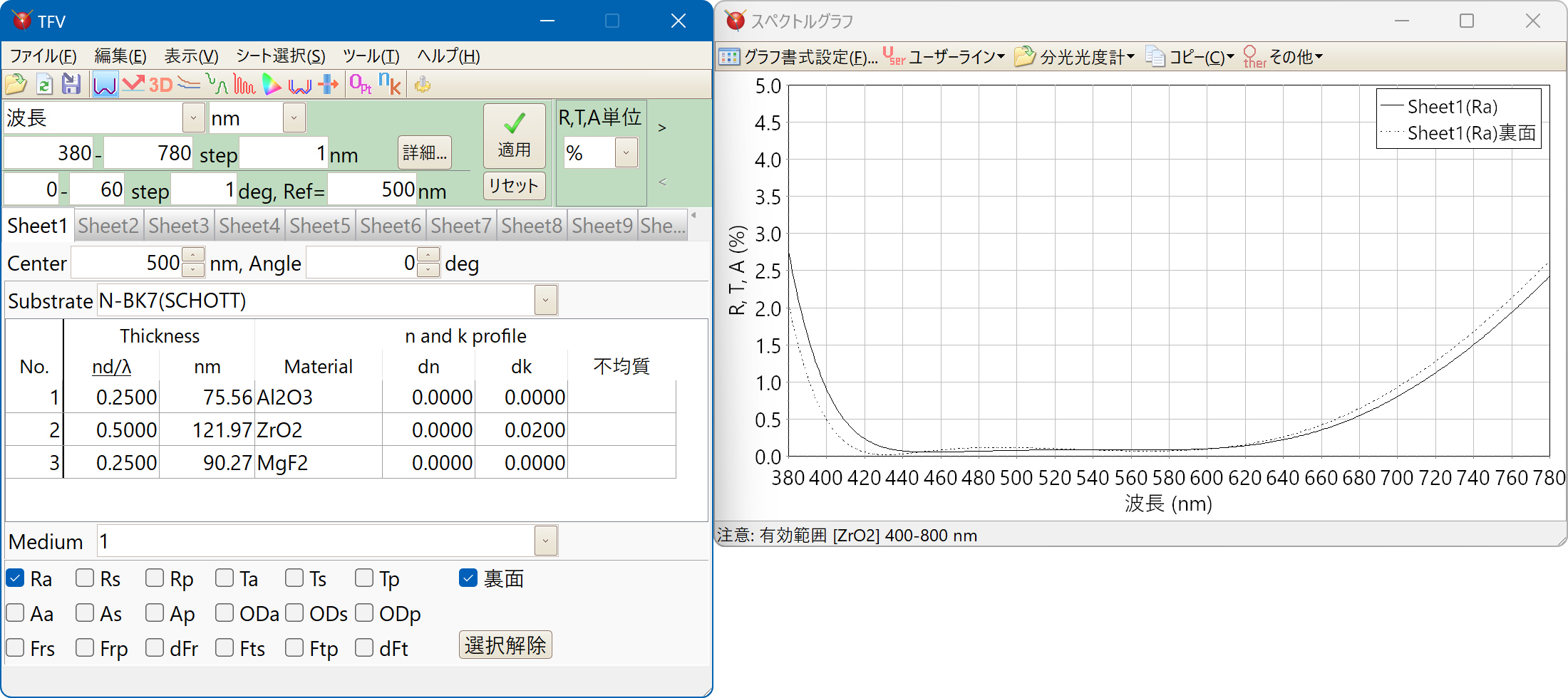
裏面側特性
表面側からの入射光の特性と裏面側からの入射光の特性を同時にグラフに表示することができます。
表面側からの入射光の光路を逆に辿った場合の特性です。
不均質
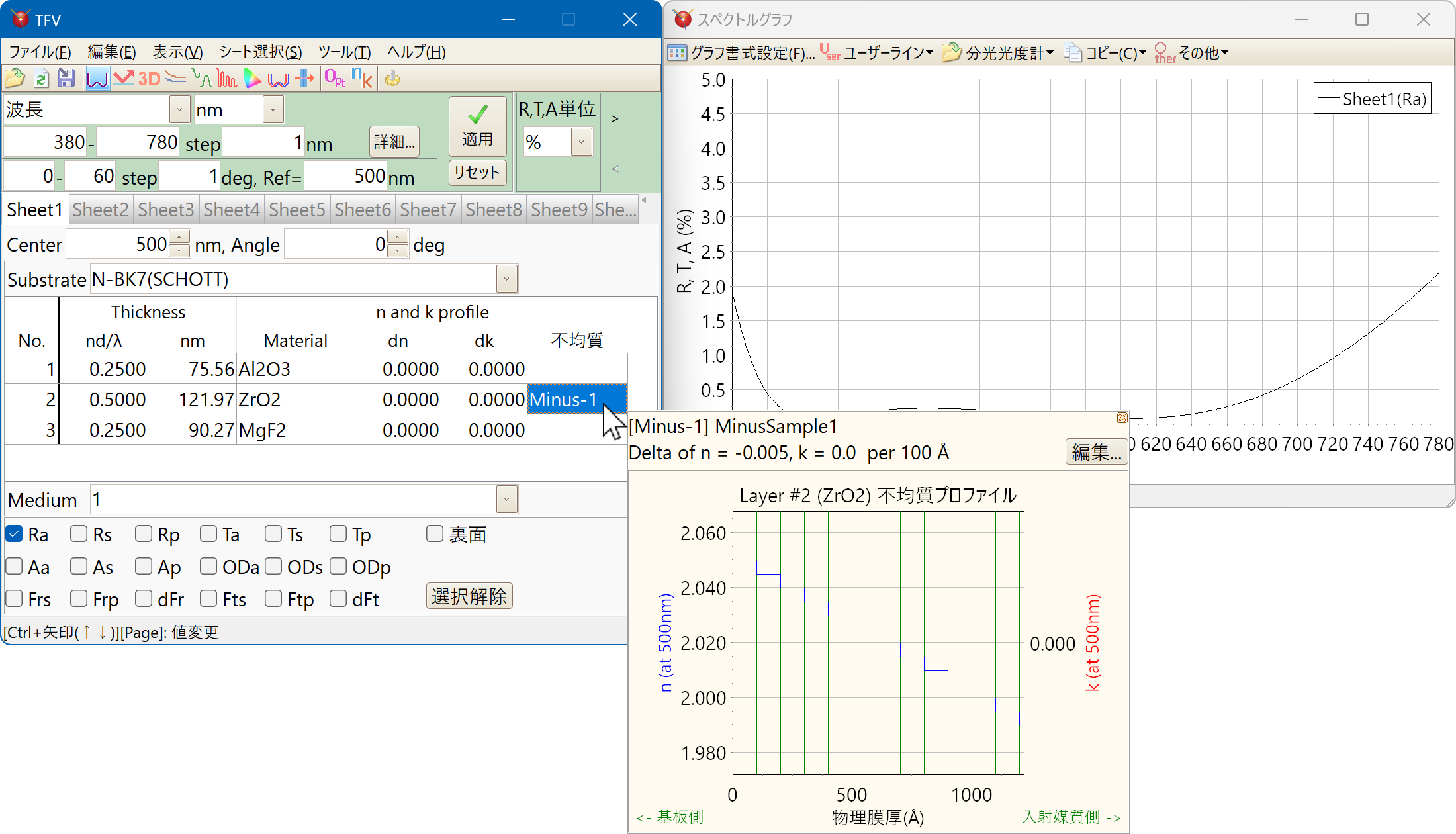
層毎に不均質を設定することができます。
負の不均質を持つZrO2膜などで、設計上の特性と実際の特性をより近づけることができます。
マウスをかざすと表示されるプレビュー画面で不均質の様子を容易に確認することができます。
周期層
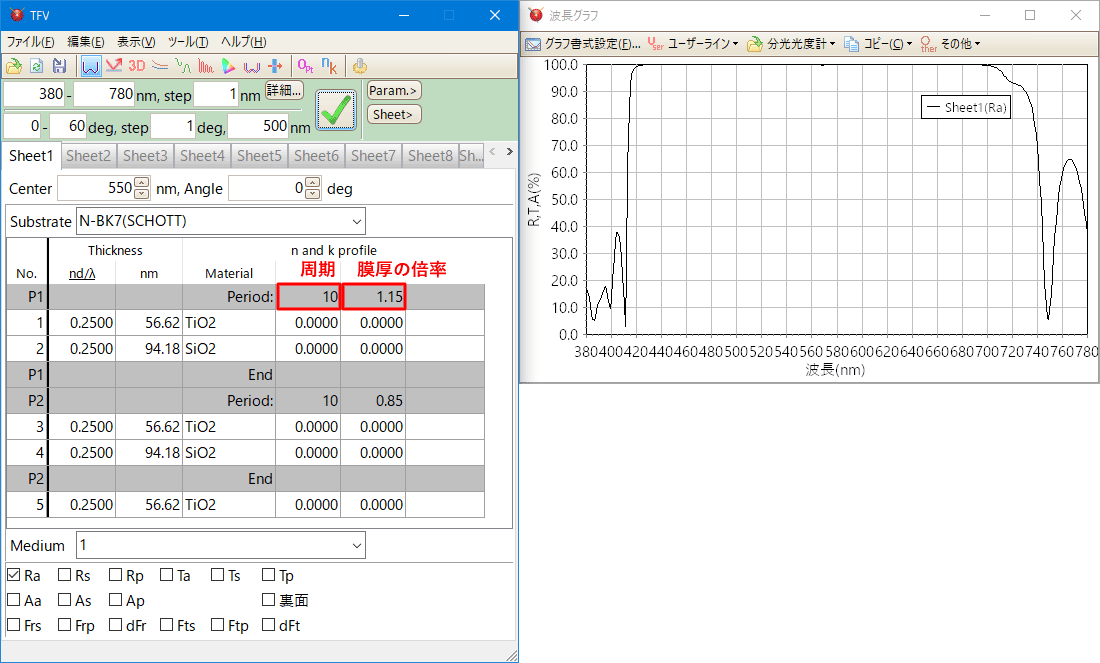
周期層をわかりやすく表示できます。
周期層内の膜厚の倍率を設定することができるため、膜厚を少しずらした周期層を重ねる設計などの検討が容易にできます。
最適化
ローカルサーチ・グローバルサーチ・ニードルサーチの3種類の最適化手法が利用できます。
グラフに表示した分光光度計データーをターゲットとして選択できるので、設計値と実測値との膜厚の差を簡単にシミュレーションすることができます。
最適化(1) 標準モード
- ローカルサーチ
-
層数固定で膜厚を最適化します。結果を1つだけ表示します。
レーベンバーグ・マーカート法(Levenberg-Marquardt Method)を用いて、膜厚を変更しながら最適解を探索します。
- グローバルサーチ
-
層数固定で膜厚を最適化します。複数の結果を表示します。
焼きなまし法(Simulated Annealing Method)とレーベンバーグ・マーカート法を組み合わせた手法を用いて、ローカルサーチの途中で膜厚をランダムに変更し、本来の解ではない局所解に陥るのを回避します。
- ニードルサーチ
-
層を増やしながら最適化します。
針状の薄い層を挿入しながら多層膜を成長させ、解を探索します。
ニードル層の挿入→ローカルサーチ→ニードル層の挿入→ローカルサーチ というサイクルを繰り返します。
最適化(2) フリーハンドモード
フリーハンドモードは、グラフ上の特性をマウスでなぞって変形させると、その変形させた形になるようにローカルサーチで最適化をおこなう、TFV独自の最適化方法です。
特許取得。
基板と薄膜のnk解析
分光光度計で測定した分光反射率・分光透過率から基板や膜のnkを計算します。
ステップ形式で画面の指示に従うわかりやすい操作性です。
- 吸収がない基板の屈折率(n)を計算
基板の片面反射率、両面反射率、透過率のいずれかから屈折率を計算します。 - 吸収がある基板の屈折率(n)、吸収係数(k)、内部透過率(Ti)を計算
基板の反射率または透過率から基板のn, k, Tiを計算します。
片面マット基板と、両面研磨基板の両方の測定値が必要です。 - 単層膜のnk解析
単層膜の屈折率(n)・吸収係数(k)・膜厚(d)を解析します。
厚い膜を付けて包絡線からnkを求める方式ではなく、分散式を分光特性にフィッティングする方式なので、λ/4~λ/2程度の実際に使う膜厚で解析ができます。 - 単層金属薄膜のnk計算
表面反射率と裏面反射率から金属膜のnkを計算します。
膜が十分に厚く、透過率が0であることが必要です。
分光光度計データー読込
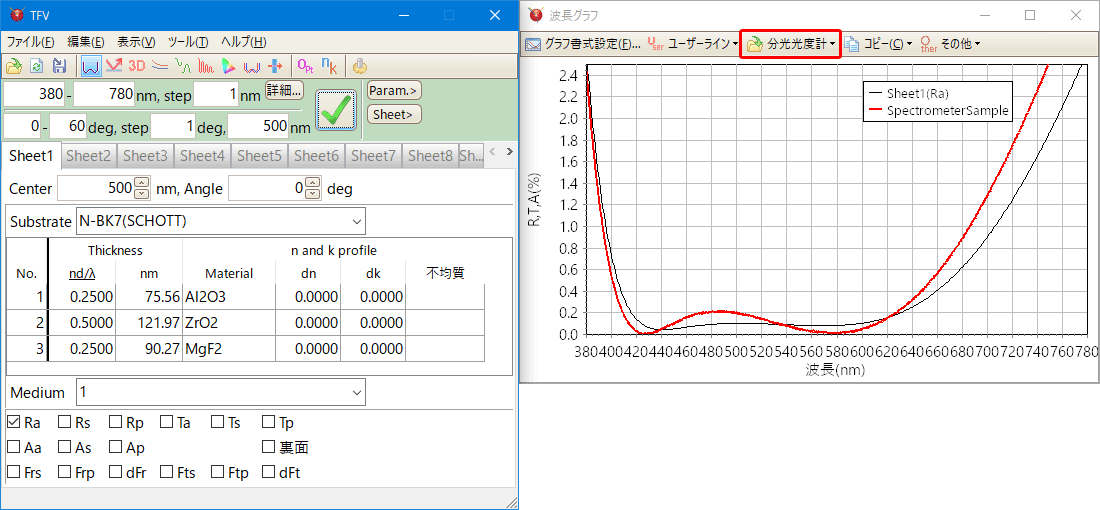
分光光度計で測定したデーターファイルを読み込んで波長グラフに表示することができます。
設計値と実測値を比較した調査に便利に利用できます。
分光光度計の測定値が相対反射の場合でも絶対反射に変換して読み込むことができます。
- 対応している分光光度計ファイル形式
-
日立分光光度計 UV-SolutionsおよびUV1ファイル(*.UDSS, *.UDS, *.UDA, *.UV1) U-4000シリーズ等
島津製作所分光光度計 SPCファイル
オリンパス レンズ反射率測定機 USPMファイル(*.dat, *.csv)
日本分光 JWSファイル
Ocean Optics ファイバー式分光器 OOi-Base32ファイル
csvファイル
タブ区切りテキストファイル
分散データー
基板データー
- ガラスを中心に、1381種類の基板データーが登録されています。
-
SCHOTT, OHARA, HOYA, SUMITA(住田光学ガラス), HIKARI(光ガラス), CDGM(成都光明)
APEL, ZEONEX, PMMA, Polycarbonate, 他
お客様独自のデーターも登録できます。
膜物質データー
- 下記の33種類の膜物質データーが登録されています。
-
Ag, Al2O3, AL, Au, Cr, Cu, H2, H4, LaF3, M3, M3-RT, MgF2, Nb2O5, Nb2O5-RT, OH5, OH5-RT, OS50, OS50-RT, SiO2, Ta2O5, Ta2O5-RT, Ti, TiO2, Zn, ZnS, ZrO2, Cytop
-
Al2O3(KTM), HfO2(KTM), LaF3(KTM), Ti3O5(KTM), ZrO2(KTM), ZRT2(KTM)
KTM: 三和研磨工業(京都薄膜材料研究所) - お客様独自のデーターも登録できます。
対応している分散式
屈折率(n)の分散式
-
Sellmeier
\[n(λ) = \sqrt{ 1 + {A_0λ^2 \over λ^2-A_3} + {A_1λ^2 \over λ^2-A_4} + {A_2λ^2 \over λ^2-A_5} } \] -
Sellmeier2
\[n(λ) = \sqrt{ 1 + A_0 + {A_1λ^2 \over λ^2-{A_3}^2} + {A_2 \over λ^2-{A_4}^2} } \]※ A2にλ2は付きません。
-
Sellmeier3
\[n(λ) = \sqrt{ 1 + {A_0λ^2 \over λ^2-A_4} + {A_1λ^2 \over λ^2-A_5} + {A_2λ^2 \over λ^2-A_6} + {A_3λ^2 \over λ^2-A_7} } \] -
Sellmeier4
\[n(λ) = \sqrt{ A_0 + {A_1λ^2 \over λ^2-A_3} + {A_2λ^2 \over λ^2-A_4} } \] -
Sellmeier5
\[n(λ) = \sqrt{ 1 + {A_0λ^2 \over λ^2-A_5} + {A_1λ^2 \over λ^2-A_6} + {A_2λ^2 \over λ^2-A_7} + {A_3λ^2 \over λ^2-A_8} + {A_4λ^2 \over λ^2-A_9} } \] -
SellmeierT1
\[n(λ) = \sqrt{ A_0 + {A_1λ^2 \over λ^2-A_2} } \] -
SellmeierT2
\[n(λ) = \sqrt{ A_0 + {A_1λ^2 \over λ^2-A_2} + A_3λ^2 } \] -
SellmeierX1
\[n(λ) = \sqrt{ 1 + {A_0λ^2 \over λ^2-{A_3}^2} + {A_1λ^2 \over λ^2-{A_4}^2} + {A_2λ^2 \over λ^2-{A_5}^2} } \] -
General1
\[n(λ) = \sqrt{ A_0 + A_1λ^2 + {A_2 \over λ^2} + {A_3 \over λ^4} + {A_4 \over λ^6} + {A_5 \over λ^8} + A_6λ^4 } \] -
General2 (Old Schott)
\[n(λ) = \sqrt{ A_0 + A_1λ^2 + {A_2 \over λ^2} + {A_3 \over λ^4} + {A_4 \over λ^6} + {A_5 \over λ^8} } \] -
Cauchy
\[n(λ) = A_0 + {A_1 \over λ^2} + {A_2 \over λ^4} \] -
Hartmann1
\[n(λ) = A_0 + {A_1 \over λ - A_2} \] -
Hartmann2
\[n(λ) = A_0 + {A_1 \over (λ - A_2)^2} \] -
Herzberger
\[n(λ) = A_0 + A_1 λ^2 + {A_2 \over (λ^2 - 0.168^2)} + {A_3 \over (λ^2 - 0.168^2)^2} \] -
Herzberger2
\[n(λ) = A_0 + {A_1 \over (λ^2 - 0.028)} + {A_2 \over (λ^2 - 0.028)^2} + A_3 λ^2 + A_4 λ^4 + A_5 λ^6 \] -
QUAD
\[n(λ) = A_0 + {A_1 \over λ^2} \] -
QUADSK
\[n(λ) = A_0 + A_1 λ + A_2 λ^2 \] -
Conrady
\[n(λ) = A_0 + {A_1 \over λ} + {A_2 \over λ^{3.5}} \] -
Handbook1 (Handbook of Optics)
\[n(λ) = \sqrt{ A_0 + {A_1 \over (λ^2 - A_2)} - A_3λ^2 } \] -
Handbook2 (Handbook of Optics)
\[n(λ) = \sqrt{ A_0 + { A_1 λ^2 \over (λ^2 - A_2)} - A_3λ^2 } \] -
Extended (ZEMAX)
\[n(λ) = \sqrt{ A_0 + A_1λ^2 + {A_2 \over λ^2} + {A_3 \over λ^4} + {A_4 \over λ^6} + {A_5 \over λ^8} + {A_6 \over λ^{10}} + {A_7 \over λ^{12}} } \] -
Extended2 (ZEMAX)
\[n(λ) = \sqrt{ A_0 + A_1λ^2 + {A_2 \over λ^2} + {A_3 \over λ^4} + {A_4 \over λ^6} + {A_5 \over λ^8} + A_6 λ^4 + A_7 λ^6 } \] -
Extended3 (ZEMAX)
\[n(λ) = \sqrt{ A_0 + A_1λ^2 + A_2λ^4 + {A_3 \over λ^2} + {A_4 \over λ^4} + {A_5 \over λ^6} + {A_6 \over λ^8} + {A_7 \over λ^{10}} + {A_8 \over λ^{12}} } \] -
Buchdahl
\[n(λ) = A_0 + A_1 ω(λ) + A_2 ω(λ)^2 \] \[ω(λ) = { λ - A_3 \over 1 + 2.5(λ - A_3) } \] -
DRUDE
\[{n^2}(λ) - {k^2}(λ) = A_0 - { A_1 {A_2}^2 λ^2 \over λ^2 + {A_2}^2 } \] -
LorentzianK
\[n(λ) = \sqrt{ A_0 + {k^2}(λ) + A_1 λ^2 {(λ^2 - {A_2}^2) \over (λ^2 - {A_2}^2)^2 + {A_3}^2 λ^2 } } \] -
Forouhi-Bloomer
\[n(E) = n(∞) + {B_0E+C_0 \over E^2 - BE + C} \] \[B_0 = {A \over Q}{({-B^2 \over 2} + E_gB - {E_g}^2 + C)} \] \[C_0 = {A \over Q}{\left(({E_g}^2 + C){B \over 2}-2E_gC\right)} \] \[Q = {1 \over 2}{(4C-B^2)}^{1 \over 2} \] \[E= {{hc} \over λ} \]h: プランク定数, c: 光速, Eの単位はeV
n(∞), Eg, A, B, C: 物質固有のパラメーター(分散式の係数) -
A0, A1, A2, A3, A4, A5, A6, A7, A8, A9は物質により定まる定数。
λの単位はμm (Forouhi-Bloomerを除く)。
吸収係数(k)の分散式
-
Sellmeier
\[k(λ) = {\biggl[ n(λ) \biggl(B_0 λ + {B_1 \over λ} + {B_2 \over λ^3} \biggr) \biggr]}^{-1} \] -
Cauchy
\[k(λ) = B_0 + {B_1 \over λ^2} + {B_2 \over λ^4} \] -
Exponential
\[k(λ) = B_0 \cdot exp(B_1 λ^{-1}) \] -
QUADSK
\[k(λ) = B_0 + B_1 λ + B_2 λ^2 \] -
DRUDE
\[2n(λ)k(λ) = { A_1 A_2 λ^3 \over λ^2 + {A_2}^2 } \] -
LorentzianK
\[k(λ) = \sqrt{ {0.5 \over n(λ)} \cdot {A_1 A_3 λ^3 \over (λ^2 - {A_2}^2)^2 + {A_3}^2 λ^2 } } \] -
Forouhi-Bloomer
\[k(E) = {A(E-E_g)^2 \over {E^2 - BE + C}} \] \[E= {{hc} \over λ} \]h: プランク定数, c: 光速, Eの単位はeV
Eg, A, B, C: 物質固有のパラメーター(分散式の係数) -
B0, B1, B2は物質により定まる定数。
λの単位はμm (Forouhi-Bloomerを除く)。
薄膜電卓(TFVMisc)
薄膜の簡単な計算をおこなうツールが付属しています。
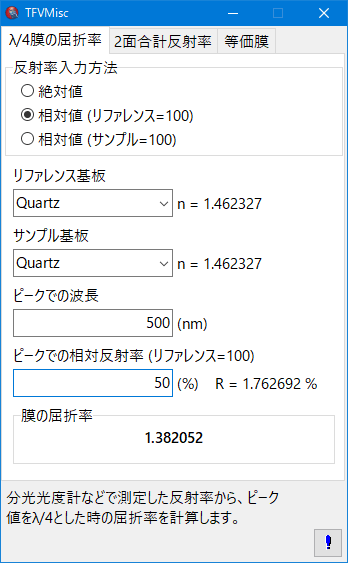
λ/4膜の屈折率計算
単層膜の反射率ピーク値から膜の屈折率を計算します。
測定値が相対反射の場合や、相対反射でリファレンスとサンプルを逆に置いた場合でも計算できます。
厚膜の反射率計算
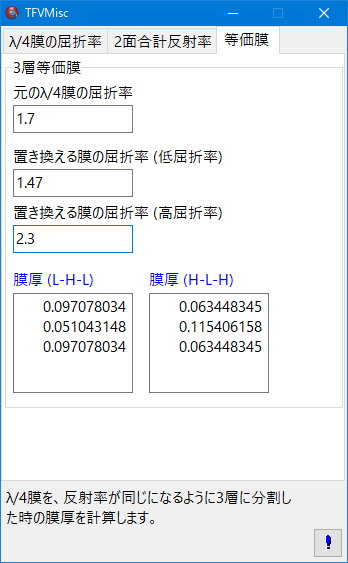
3層等価膜計算
λ/4膜を、反射率が同じになるように別の2種類の屈折率の3層膜に置き換えます。